previous  page PLNT4610/PLNT7690 Bioinformatics
Lecture 4, part 2 of 2		 next page

C. Global and local optimal alignments


 A
 A
 C
 T
 G
 T
 T
A
 1





A
2




C

3



T


4


G



5

T




6
T





7
While dot-matrix searches provide a great deal of information in a visual fashion, they can only be considered semi-quantitative, and therefore do not lend themselves to statistical analysis. Also, dot-matrix searches do not provide an alignment between two sequences.   For the trivial case of scoring two sequences that are identical, one could simply add +1  to the score for each match. The longer the similarity, the higher the score, and the more significant the similarity would be. The example at right shows that a perfect  identity between two sequences 7 nt long, the resultant score would be 7.

Global alignment by dynamic programming extends the dot-matrix concept to give, for any possible path through the matrix, a score that takes into account mismatches and gaps.
 

1. Global sequence alignment by dynamic programming

 Setubal, J. and Meidanis, J. (1997) Introduction to Computational Molecular Biology. PWS Publishing Co., Toronto. Ch. 3 "Sequence Comparison and Database Search".

Sequence alignment methods predate dot-matrix searches, and all of the alignment methods in use today are related to the original method of Needleman and Wunsch (1970). Needleman and Wunsch wanted to quantify the similarity between two sequences. Over the course of evolution, some positions undergo base or amino acid substitutions, and bases or amino acids can be inserted or deleted. Any measurement of similarity must therefore be done with respect to the best possible alignment between two sequences. Because insertion/deletion events are rare compared to base substitutions, it makes sense to penalize gaps more heavily than mismatches when calculating a similarity score.  As an example, a very simple scoring scheme would add +1 for each match, -1 for each mismatch, and -2 for each gap inserted. That is, the larger the gap, the more we subtract. The similarity between two sequences would then be

Similarity = +1(# identities) -1(#mismatches) -2(#gaps)
For example: 
          GCTGGAACCAG
           |||||  |||
          ACTGGAT-CAG
                      Similarity = 1(8) - 1(2) -2(1) = 4

By definition, the alignment which gives the higest similarity score is the optimal alignment. However, the number of alignments that must be checked  increases exponentially with the lengths of the sequences. Allowing gaps also results in an exponential increase in the computation time required.

Although the problem may seem intractably large for all but very small sequences, Needleman and Wunsch conceptualized alignment as a problem in dynamic programming, in which the solution to a large problem is simplified if we first know the solution to a smaller problem that is a subset of the larger problem. Think of an alignment occurring in a matrix, where sequence s of length m is written on the Y-axis, and sequence t  of length n is written on the X-axis. The alignment can then be acomplished in two steps:

1. All possible alignments of s and t are contained in array a[0..m,0..n] (the component a[0,0] represents a gap at the beginnning of each sequence).

2. The optimal alignment will be the path through the array that has the highest score, ie. the largest number of matches and fewest mismatches and gaps.

Needleman and Wunch realized that all parts of the alignment problem boiled down to the same decision made at every position i in sequence s,  when compared with every position j in sequence t.

If we want to calculate the score at  any position a[i,j] in the alignment matrix a, we only have to look at three adjacent cells in the matrix to calculate that score, a[i,j-1], a[i-1,j-1], or a[i-1,j]. These are the positions in the alignment that represent the part of the alignment just prior to a[i,j], at which point either:

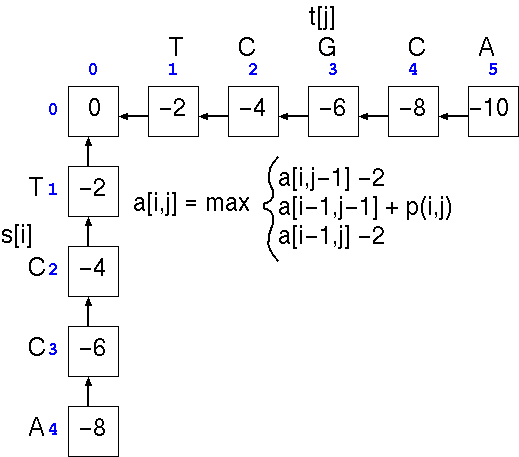
This simple formula can be used to calculate partial alignment scores at all parts of the alignment matrix.

Step 1 - Calculation of the alignment matrix

The first step is the trivial calculation of the case in which one or more terminal gaps are added to the beginning of either sequence. This is done by running across the top of the array and progressively adding a gap penalty (eg. -2) to the score in each cell, and doing the same to the leftmost column. Next, we apply the three scoring rules to each cell in the matrix.

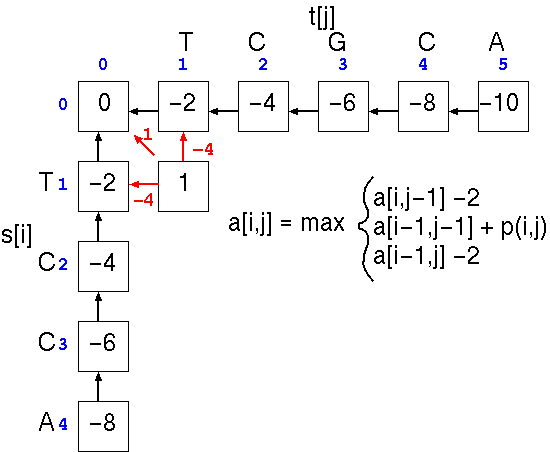
At cell a[1,1], the score is the largest of three possible scores

where p(i,j) is a function that returns +1 if s[i] = t[j] (match) or -1 if s[i] ¬ = t[j].

This process is repeated down the matrix:

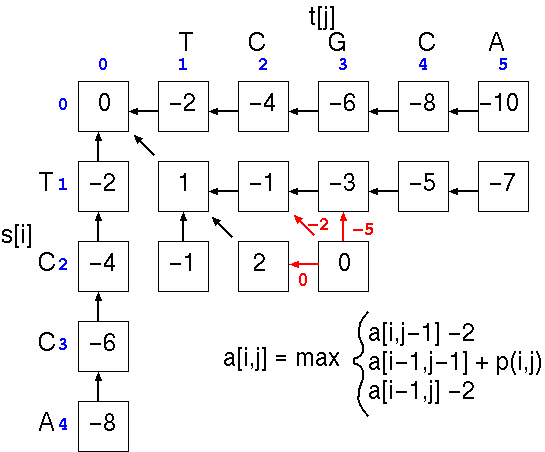
until all cells are filled.

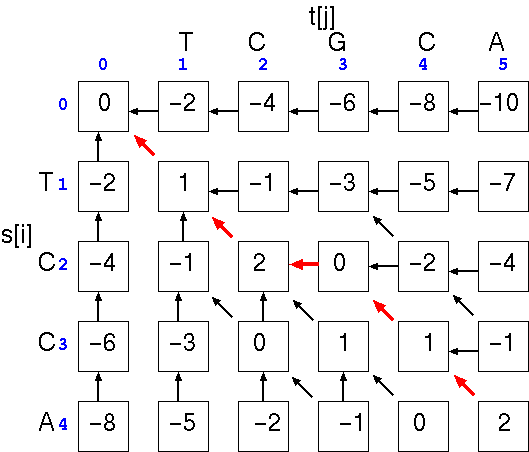
Step 2 - Construction of the optimal alignment

The final example shows the completed array, with arrows pointing from each cell to one adjacent cell (ie. the cell that gave the highest score) or more than one adjacent cell in case of a tie. Since the path to the highest scoring adjacent cell (s) is always known, we can start at the last position in the alignment, a[m,n], and work backwards to the beginning, a[1,1], adding scores along a fairly limited number of alternative paths.

The optimal alignment will be the path that gives the highest total score. In the example, the optimal alignment would be 

TCGCA
|| ||
TC-CA
and the similarity score is simply the score at cell a[i,j], the last cell in the alignment. We can check the score by using the written alignment: 4(+1) + 0(-1) + 1(-2) = 2.


Note that if we hadn't inserted the gap, the alignment would be 

TCGCA
|| 
TCCA-
and the similarity score at cell a[i,j], would be: 2(+1) + 2(-1) + 1(-2) = -2. The point is that a single gap can make a large difference in the score.

Though these examples give the essence of the Needleman Wunsch method, the literature contains a wealth of papers improving on this simple algorithm.

Example of an optimal alignment between cDNA sequences for defensin genes from Pea (PPEADRR230B) and Cucumber (CAGT).

The alignment was produced by GLSEARCH from the FASTA package.

n-w opt: The raw Needleman-Wunch alignment score

Z-score: Standard Deviations of the best score relative to the mean of all alignments tested.

bits: Measure of information content of the alignment ie. how it differs from a random alignment.

E: Probability of seeing an alignment this good by comparing two arbitrary sequences of similar nucleotide content.
 
Statistics: (shuffled [500]) Unscaled normal statistics: mu= -90.3780  var=579.7105 Ztrim: 0
 statistics sampled from 1 (1) to 500 sequences
Algorithm: Global/Local affine Needleman-Wunsch (SSE2, Michael Farrar 2010) (6.0 April 2007)
Parameters: +5/-4 matrix (5:-4), open/ext: -12/-4
 Scan time:  0.040

The best scores are:                                      n-w bits E(1)
PEADRR230B:CDS1 225 bp                         ( 225) [f]   60 28.0 2.1e-10

>>PEADRR230B:CDS1 225 bp                                  (225 nt)
 n-w opt:  60  Z-score: 112.5  bits: 28.0 E(1): 2.1e-10
global/local score: 60; 51.9% identity (51.9% similar) in 231 nt overlap (1-228:16-225)

                              10        20        30        40     
CAGT:C                ATGGCTGGCTTTTCCAAAGTAGTTGCAACTATTTTTCTTATGATG
                       : :::: ::: :::    :  :  :  ::  :: ::::    ::
PEADRR ATGGAGAAGAAATCACTAGCTGCCTTGTCCTTCCTCCTC-CTCCTCGTTCTCTT----TG
               10        20        30         40        50         

          50        60        70        80        90       100     
CAGT:C TTGCTGGTTTTTGCTACTGATATGATGGCGGAGGCAAAGATCTGCGAGGCGTTGAGCGGC
       ::::        :  : ::   :: :: : :::::::: :  :: :::   :::   :  
PEADRR TTGCACAA----GAAATTG---TGGTGACAGAGGCAAACACTTGTGAGCATTTGGCTGAT
          60            70           80        90       100        

         110       120       130       140       150        160    
CAGT:C AACTTCAAGGGGTTGTGCCTTAGTAGCCGCGATTGTGGTAATGTTTGCC-GTAGAGAGGG
       :  : :: :::  : ::: : :  :        :::: : ::   :::  : : : :: :
PEADRR ACATACAGGGGAGTATGCTTCACGAATGCTAGCTGTGATGATCACTGCAAGAACAAAGCG
      110       120       130       140       150       160        

            170       180       190       200       210       220  
CAGT:C A--TTTACCGATGGCTCTTGCATTGGATTCCGTCTTCAATGCTTCTGCACGAAGCCCTGT
          :: : :  :::: : :::  ::  :         :::: ::::::::  :   ::: 
PEADRR CACTTAATCAGTGGCACGTGCCATGACTGGA------AATGTTTCTGCACTCAAAACTG-
      170       180       190             200       210       220  

             
CAGT:C GCTTAA
         ::::
PEADRR --TTAA

2. Local sequence alignment by the Smith-Waterman method

Forcing the entire length of both sequences into alignment may not be a realistic representation of the similarity. In most cases, only a particular block of nucleotides or amino acids have a compelling degree of similarity, while flanking regions may not. As well, considering regions out side the homologous region requires extra computational space and time, which we recall increases with the square of the length.

For these reasons Smith and Waterman developed a modification of the NW algorithm, now referred to as SW. In essence, when SW encounters a negative score at any point in the matrix, it sets the score of that x,y cell to 0. The result of setting this score to 0 is to prevent the algorithm from trying to extend into regions that would negatively contribute to the score.  The following table summarizes the differences between NW and SW.



 Smith–Waterman algorithm Needleman–Wunsch algorithm
Initialization First row and first column are set to 0 First row and first column are subject to gap penalty
Scoring Negative score is set to 0 Score can be negative
Traceback Begin with the highest score, end when 0 is encountered Begin with the cell at the lower right of the matrix, end at top left cell

from https://en.wikipedia.org/wiki/Smith%E2%80%93Waterman_algorithm

Significance: SW drastically speeds up the NW algorithm by eliminating flanking regions which cannot possibly improve the alignment, resulting in a local alignment with the same rigor as the exhaustive NW algorithm.

A Word on Affine Gap Penalties

From an evolutionary point of view, the gap penalty scheme in the simple Needleman-Wunsch algorithm is highly unrealistic. Although single point insertions or deletions ("indels") are probably more common than large indels, it is not obvious that any sort of linear relation exists between frequency of indels and length. That is, it's just as easy to delete 4 bases as to delete 2. Most alignment programs deal with this problem using affine gap penalties. Affine gap penalties consist of an "open gap" penalty to begin an indel, and an "extend gap" penalty for each subsequent gap character inserted into the alignment. Typically, the open gap penalty is much larger than the extend gap penalty. Unfortunately, there is no empirical data to guide the choice of values for these penalties.

Affine gap penalties are calculate by the formula:
penalty = gap_begin + (# gaps * gap_extend)
Example: For a 2 base gap in a DNA pairwise alignment, if gap_begin = -10 and gap_extend=-1, the gap penalty is -10 + 2(-1) = -12.

3. Scoring matrices

Pearson WR (2013) Selecting the Right Similarity-Scoring Matrix. Curr Protoc Bioinformatics. 2013; 43: 3.5.1–3.5.9.
10.1002/0471250953.bi0305s43

Matricies borrowed from: Hugh B. Nicholas Jr., David W. Deerfield II., and Alexander J. Ropelewski"A Tutorial on Searching Sequence Databases and Sequence Scoring Methods", Biomedical Supercomputing Initiative of the Pittsburgh Supercomputing Center [http://www.nrbsc.org/education/tutorials/sequence/db ].

Construction of biologically significant alignments should take into account the fact that protein evolution is constrained by the chemical properties of amino acids, and by the degeneracy of the genetic code. Chemically conservative replacements tend to occur more frequently than  replacements with amino acids that are chemically different. For example, it is far more likely to see a substitution of Leucine with Isoleucine, both of which are non-polar, than a substitution of Aspartic acid, which is negatively-charged, for Leucine.

Secondly, the observed frequencies of substitution will depend on the genetic code. Amino acid substitutions that require only a single nucleotide replacement will occur more frequently than substitutions requiring 2 or 3 nucleotide replacements.

Scoring matrices have been constructed to replace the p(i,j) function above. That is, for any possible amino acid substitution, a value from the scoring matrix is added to the similarity score, rather than adding 1 for an identity and -1 for a mismatch. One of the most commonly-used scoring matrices is the PAM250 matrix, shown below:


PAM 250 Amino Acid Similarity Matrix

Cys  12
Gly  -3   5
Pro  -3  -1   6
Ser   0   1   1   1
Ala  -2   1   1   1   2
Thr  -2   0   0   1   1   3
Asp  -5   1  -1   0   0   0   4
Glu  -5   0  -1   0   0   0   3   4
Asn  -4   0  -1   1   0   0   2   1   2
Gln  -5  -1   0  -1   0  -1   2   2   1   4
His  -3  -2   0  -1  -1  -1   1   1   2   3   6
Lys  -5  -2  -1   0  -1   0   0   0   1   1   0   5
Arg  -4  -3   0   0  -2  -1  -1  -1   0   1   2   3   6
Val  -2  -1  -1  -1   0   0  -2  -2  -2  -2  -2  -2  -2   4
Met  -5  -3  -2  -2  -1  -1  -3  -2   0  -1  -2   0   0   2   6
Ile  -2  -3  -2  -1  -1   0  -2  -2  -2  -2  -2  -2  -2   4   2   5
Leu  -6  -4  -3  -3  -2  -2  -4  -3  -3  -2  -2  -3  -3   2   4   2   6
Phe  -4  -5  -5  -3  -4  -3  -6  -5  -4  -5  -2  -5  -4  -1   0   1   2   9
Tyr   0  -5  -5  -3  -3  -3  -4  -4  -2  -4   0  -4  -5  -2  -2  -1  -1   7  10
Trp  -8  -7  -6  -2  -6  -5  -7  -7  -4  -5  -3  -3   2  -6  -4  -5  -2   0   0  17
     Cys Gly Pro Ser Ala Thr Asp Glu Asn Gln His Lys Arg Val Met Ile Leu Phe Tyr Trp
Substitution of an Aspartic acid for Glutamic acid (both acidic) adds 3 to the score. Substitution of the positively-charged Lys for the non-polar Pro adds -1 to the score.  Generally, the more conservative the replacement, the higher the value that will be added to the score.

Substitution matrices like PAM250 are constructed by observing the frequencies of amino acid replacements in large samples of protein sequences. For a given replacement, the PAM value is proportional to the natural log of the frequency with which that replacement was observed to occur.

The Blosum series of matrices are also commonly-used.


Blosum 45 Amino Acid Similarity Matrix

Gly   7
Pro  -2   9
Asp  -1  -1   7
Glu  -2   0   2   6 
Asn   0  -2   2   0   6
His  -2  -2   0   0   1  10
Gln  -2  -1   0   2   0   1   6
Lys  -2  -1   0   1   0  -1   1   5
Arg  -2  -2  -1   0   0   0   1   3   7
Ser   0  -1   0   0   1  -1   0  -1  -1   4
Thr  -2  -1  -1  -1   0  -2  -1  -1  -1   2   5
Ala   0  -1  -2  -1  -1  -2  -1  -1  -2   1   0   5
Met  -2  -2  -3  -2  -2   0   0  -1  -1  -2  -1  -1   6
Val  -3  -3  -3  -3  -3  -3  -3  -2  -2  -1   0   0   1   5
Ile  -4  -2  -4  -3  -2  -3  -2  -3  -3  -2  -1  -1   2   3   5
Leu  -3  -3  -3  -2  -3  -2  -2  -3  -2  -3  -1  -1   2   1   2   5
Phe  -3  -3  -4  -3  -2  -2  -4  -3  -2  -2  -1  -2   0   0   0   1   8
Tyr  -3  -3  -2  -2  -2   2  -1  -1  -1  -2  -1  -2   0  -1   0   0   3   8
Trp  -2  -3  -4  -3  -4  -3  -2  -2  -2  -4  -3  -2  -2  -3  -2  -2   1   3  15
Cys  -3  -4  -3  -3  -2  -3  -3  -3  -3  -1  -1  -1  -2  -1  -3  -2  -2  -3  -5  12
     Gly Pro Asp Glu Asn His Gln Lys Arg Ser Thr Ala Met Val Ile Leu Phe Tyr Trp Cys


One criticism of the PAM matrices is that the PAM units were calibrated using pairs of closely-related proteins, because these could be aligned by hand. However, PAM1 units are extrapolated to high PAM values (eg. PAM250), so it is uncertain how realistic these extrapolated values are.

The Blosum matrices were calculated using data from the BLOCKS* database [http://blocks.fhcrc.org ], which contains alignments of more distantly-related proteins. In principle, Blosum matrices should be more realistic for comparing distantly-related proteins because the matrices are derived from distantly-related proteins. On the other hand, one could argue that the more distantly related proteins are, the less reliable the alignment, which could contribute to error in the calculation of Blosum matrices.

*Note: The BLOCKS database is no longer supported. This just goes to show a chronic problem in bioinformatics - the original datasets used to build empiracally-derived computational tools become more difficult to find as the original data sinks into obsolescence.

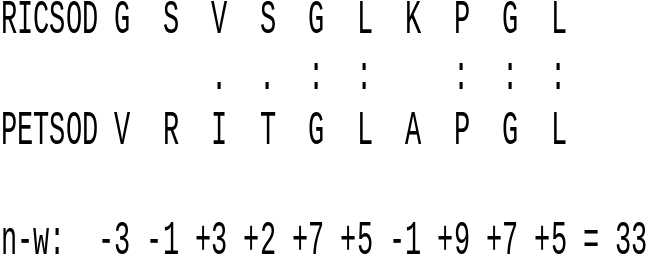
Example:  Calculation of the Needlwman-Wunsch score for a short segment of superoxide dismutase proteins from rice and parsley. The BLOSUM 45 scoring matrix was used.

: - identities
. - similar amino acids


Choosing the correct scoring matrix to use

Equivalent PAM and Blossum matrices

The following matrices are roughly equivalent...

Generally speaking...
Gap penalties for proteins

As mentioned above, there are no good theoretical criteria for choosing gap begin and gap extend penalties for proteins. That being said, we know that insertion/deletion events are less frequent than amino acid substitutions. Therefore, it makes sense that a gap begin penalty should be more negative than the lowest-scoring amino acid substitution. For example, with the PAM250 matrix, the worst possible amino acid substitution is a Trp (W) - Cys (C) substitution, which gives a score of -8. With BLOSUM45, same substitution gives a score of -5. Therefore, it would be reasonable that even a single gap that the gap_begin penalty should be greater than any possible substitution penalty.

In BLAST, the default gap penalties for protein comparisons are gap_begin = -11, gap_extend=-1

Unless otherwise cited or referenced, all content on this page is licensed under the Creative Commons License Attribution Share-Alike 2.5 Canada

previous  page PLNT4610/PLNT7690 Bioinformatics
Lecture 4, part 2 of 2		 next page