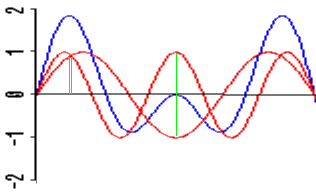
If you're listening to waves from two sources at the same time:
You can calculate the overall wave that your ears will receive by adding together the pressure of the two waves at each point in time. (You have to treat the normal background air pressure as zero, so that a higher pressure has a positive number and a lower pressure has a negative number.)

The following two sounds have frequencies of 300 Hz and 500 Hz respectively:
Added together at each moment in time, they produce the following more complex wave:
(Here are the gory details:)
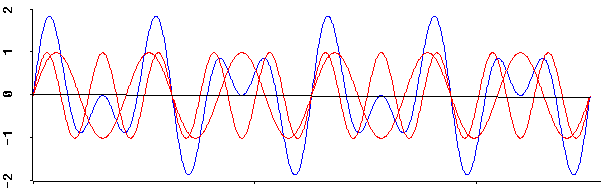
The fact that we can add simple sine waves together to form a complex wave is important because we can also do the reverse:
Any complex wave can be treated as a combination of simple sine waves.
The mathematical technique that breaks a complex wave down into its simple waves is called Fourier analysis, after the mathematician Joseph Fourier who pioneered it. Most computer programs use a simplified version of Fourier analysis called the Fast Fourier Transform (or FFT).
For most practical purposes in phonetics, we don't care about the actual complex waveform itself. We're only interested in the frequencies and amplitudes of the simple waves that it's made of.