Montgomery Pic Mia, Odlyzko Pic Mia

The year: 1972. The scene: Afternoon tea in Fuld Hall at the Institute for Advanced Study. The camera pans around the Common Room, passing by several Princetonians in tweeds and corduroys, then zooms in on Hugh Montgomery, boyish Midwestern number theorist with sideburns. He has just been introduced to Freeman Dyson, dapper British physicist.

Dyson: Extraordinary! Do you realize that's the pair-correlation function for the eigenvalues of a random Hermitian matrix? It's also a model of the energy levels in a heavy nucleus—say U-238.

"I'd never heard any of these terms before," Montgomery went on. "I don't know exactly what his words were because I have heard all of these terms many times since, but he said 'pair correlation' and something resembling 'random matrices'..."

What Dyson meant:

• The energy levels associated with a complex system are described by the Hamiltonian of the system.
  
• These systems are so complex that the Hamiltonian is not known but can be analyzed using non-deterministic methods i.e. Monte Carlo methods. 
  
• The Hamiltonians are Hermitian meaning that the diagonals are real, and the off diagonals are complex conjugates.
  
• The eigenvalues of these Hamiltonians "are" the corresponding energy levels of a complex system.
  
• The matrices are infinite and random.

The pair correlations of the Riemann zeros and the eigenvalues are not random but seem to obey the same statistics.

Figure 1. One-dimensional distributions each consist of 100 levels. From left to right the spectra are: a periodic array of evenly spaced lines; a random sequence; a periodic array perturbed by a slight random “jiggling” of each level; energy states of the erbium-166 nucleus, all having the same spin and parity quantum numbers; the central 100 eigenvalues of a 300-by-300 random symmetric matrix; positions of zeros of the Riemann zeta function lying just above the 10²²nd zero; 100 consecutive prime numbers beginning with 103,613; locations of the 100 northernmost overpasses and underpasses along Interstate 85; positions of crossties on a railroad siding; locations of growth rings from 1884 through 1983 in a fir tree on Mount Saint Helens, Washington; dates of California earthquakes with a magnitude of 5.0 or greater, 1969 to 2001; lengths of 100 consecutive bike rides.

---

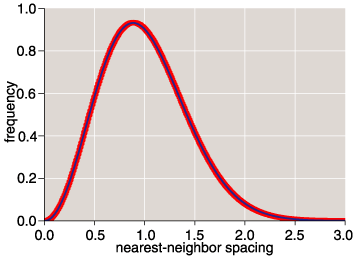
Zeros of the Riemann zeta function have nearest-neighbor spacings closely matched by the predictions of random-matrix theory. Red dots represent positions of a billion zeta zeros above the 10²³rd such zero; the blue line is the predicted spacing.

Note: it sort of resembles that of the "Central Limit Theorem". Actually the Gaussian Unitary Ensemble GUE or the Gaudin Distribution.

Over the past 20 years Andrew M. Odlyzko, now at the University of Minnesota, has taken the computation of zeta zeros to heroic heights in order to perform such tests. One of Odlyzko's early papers was titled "The 10²⁰th zero of the Riemann zeta function and 175 million of its neighbors." Since then he has gone on to compute even longer series of consecutive zeros at even greater heights, now reaching the neighborhood of the 10²³rd zero.

The correspondence is now known as the Dyson-Odlyzko-Montgomery Law

Note: The basic idea of finding an infinite dimensional matrix whose eigenvalues could correspond to the zeros of the Riemann Zeta function is actually attributed to Polya and Hilbert who in 1914 first posited this possibility. This view is that the zeros of the zeta function really do represent a spectrum—a series of energy levels just like those of the erbium nucleus, but generated by the mathematical element Riemannium.