| This tutorial assumes that you have already gone through the DNA phylogeny tutorials at http://home.cc.umanitoba.ca/~psgendb/tutorials/GDE/gde.html |
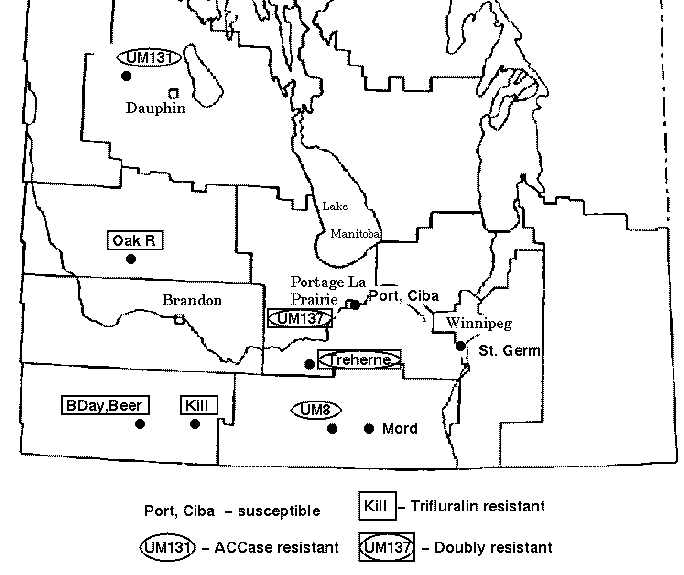
Green foxtail is a grassy weed that is commonly found in cultivated fields in the Canadian prairies. Foxtail is usually controlled in cereal crops by inhibitors of acetyl-CoA carboxylase (ACCase) such as fenoxaprop-P-ethyl or by trifuluralin. However, accessions of foxtail have been identified which are resistant to one or both types of herbicide. The map below indicates the locations of sites in the province of Manitoba where herbicide resistant green foxtail populations have been found.

Thirteen accessions of green foxtail were tested for resistance to
ACCase
inhibitor and trifluralin. These accessions were also subjected to RAPD
analysis, in which polymorphism was scored at 42 loci. The data are
represented
in Phylip format in the file manitoba.phyl.
Note: Phylip format for discrete data
|
Create a directory called foxtail, and save manitoba.phyl to
this
directory. Start mGDE by typing
mgde
To read this file into mGDE, choose File -> Import Phylip Discrete Data.
The sequences will be read into the GDE window.


Although this menu is quite the same as the distance menu for DNA and protein sequences, let's look at some important menu items:
DISTANCE MODEL: SITES/REST. FRAGS. - By default, each marker represents a distinct genetic locus. This is true for most types of molecular markers. However, for RFLPs, it is often the case that a given locus may be represented by two distinct bands, representing alleles. In this case, "REST. FRAGS." should be used.The output appears in windows as shown:SITE LENGTH - The number of nucleotide positions assayed by a marker method. For RFLP analysis using restriction enzymes with 6-base recognition sequences, this number is 6. That is, cleavage by the enzyme requires specific nucleotides must match at 6 positions. For RAPDs using primers 10 bases long, SITE LENGTH is 20 (not 10!). This is because the primer must match 10 bases on each side of the fragment to be amplified. For AFLPs, the number of selective bases is between 14 - 18 nt, depending on the restriction enzymes used. Obviously, the longer the site length, the lower the probability of a 0 -> 1 mutation. Put another way, it is much easier for a single site to mutate to match a 6 base restriction sequence than it is for two nearby sites to mutate to match a 10 base primer.
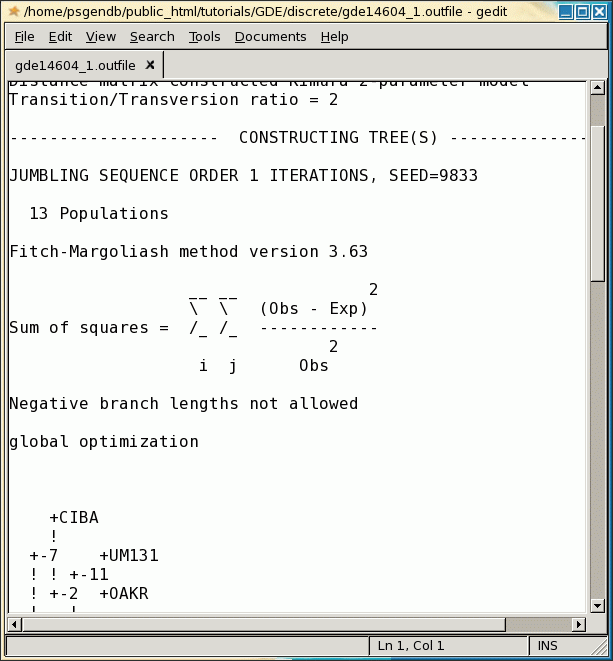
OUTFILE (manitoba.fitch.outfile)
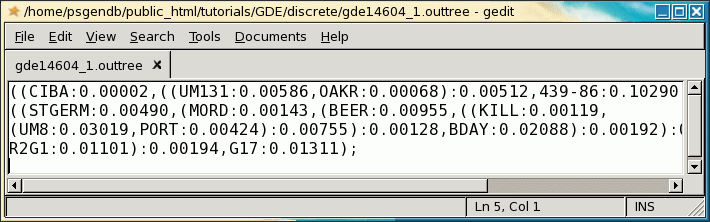
TREEFILE
(manitoba.fitch.treefile)
The output treefile is launched in two applications: a text editor,
to make it easy to save the file, and tGDE, to make it easier to work
with the tree, or to use various tree drawing programs.

ATV
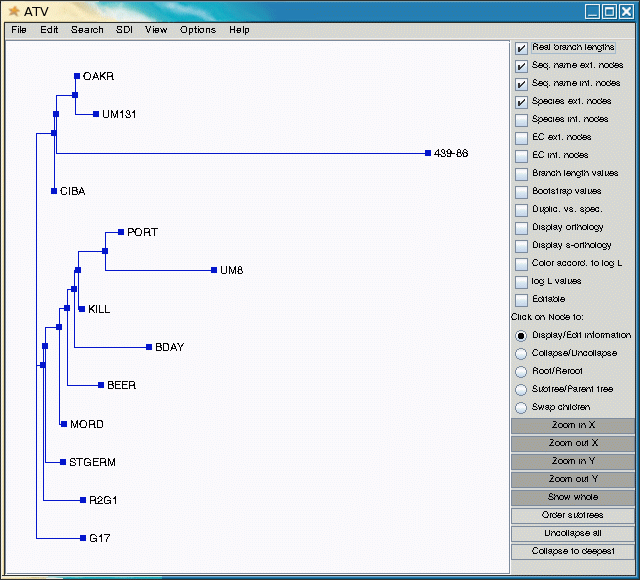
Note that accession 439-86 appears to be an outgroup, very distantly related to all other accessions. This is consistent with the fact that 439-86 originated in China, and was included as a control.
Several parsimony methods are available, as indicated in the menu:
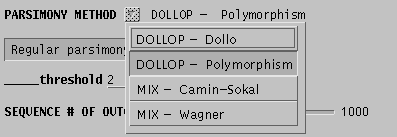
In this example, Joe Felsenstein's Polymorphism parsimony method has been chosen. This method is worthy of some mention. For most molecular marker systems, Dollo parsimony is usually the most realistic choice because it assumes that the probability of a 1 -> 0 mutation (loss of a band) is much greater than a 0 -> 1 mutation (gain of a band.) However, this model may be overly pessimistic, simply due to the fact that, if polymorphism for a given site exists, in a population (ie. both 1 AND 0 are present), a population containing both alleles might be sampled, and erroneously assigned 0, even though 1 is present in other individuals that were not sampled. Polymorphism parsimony tries to take this possibility into account. If most nodes on a branch contain 0s, but at least one 1 node is implied, the polymorphism parsimony option of dollop will assume that the presence of the 1 is due to polymorphism in the population, rather than a rare forward mutation.
For the same input data, dollop will produce the following output files:
manitoba.polymorphism.outfile
manitoba.polymorphism.treefile
When a data set is monomorphic at a given site (ie. all 0 or all 1) is it because the population is monomorphic, or is it that we simply haven't sampled enough individuals to detect polymorphism? In a populaiton monomorphic for absence of a band (ie. all 0), probability of seeing a band is zero. In a population containing 1s, if we take a sample that contains all 0's, the probabilty of 1 is most definitely not 0. We only got all 0's due to how the population was sampled. For this reason, restml defaults to No, for 'All sites detected'. For situations in which some sites may be polymorphic, but are not reflected in the data, however, choose 'Yes', all sites detected.
Caveat: I think I got this right, but it's a subtle point. See $doc/Phylip/restml.html for further explaination.
When branch lengths are being calculated, restml has to try a number of different branch lengths, for each branch, to see which is the branch length most likely to generate the observed data. Since branch lengths are real numbers, in principle, an infinite number of branches would have to be tested. In practice, restml tries a small number of possible branch lengths, starting with a short branch and multiplying its length by an extrapolation factor. A small extrapolation factor will increase the branch length slowly, requiring more iterations, but resulting in more precise branch lengths. A large extrapolation factor will require few iterations, but at the expense of precision. A "Speedier but Rougher Analysis" uses a larger extrapolation factor, and therefore sacrifices thoroughness in favor of speed.Sample output files:
manitoba.restml.outfile
manitoba.restml.treefile
| WARNING
Maximum likelihood methods are very slow, because they attempt to consider an enormous number of possible trees. The time required increases exponentially with the number of sequences. Therefore doubling the number of sequences does not double the execution time. In fact for restml, the time required increases roughly with thr 4th power of the number of the sequences! For most practical purposes, direct tree construction with greater than 30 sequences requires prohibitive amounts of time. Since bootstrapping multiplies the time required often by a
factor of
100 or more, we usually don't have the luxury of bootstrapping with
maximum
likelihood methods. However, as illustrated above, we can bootstrap
with
a less time consuming method such ase parsimony, and then build the
final
tree with Maximum Likelihood. |