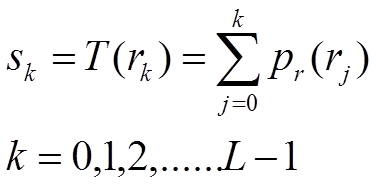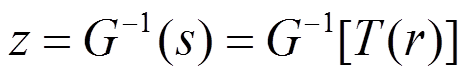The following can be found in:

 

G. Thomas, D. Flores-Tapia, and S. Pistorius, “ Histogram Specification: a Fast and Flexible Method to Process Digital Images,” IEEE Trans. Instrumentation and Measurement Vol. 60, No. 5, pp: 1565-1578,  2011.

 

There is Matlab code that implements Brightness Preserving Histogram Equalization with Maximum Entropy but using an iterative approach

 

Contrast Enhancement by
Histogram Equalization

•          Modify an image such that its histogram has a uniform distribution.

•          The transformation s=T(r) needed to obtain this equalization can be formulated as

 

 

 


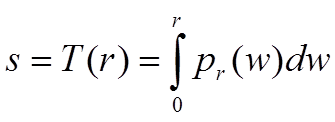
•          where r is the intensity value of the original pixel,

•          s is the pixel value of the transformed image,

•          and pr(r) is the Probability Density Function PDF associated to the original image

•          In its discrete form becomes                                  

               

 

 

 

•          for an image with L gray level values.

                

 

Uniform histogram is not necessarily the best result
 


 

 

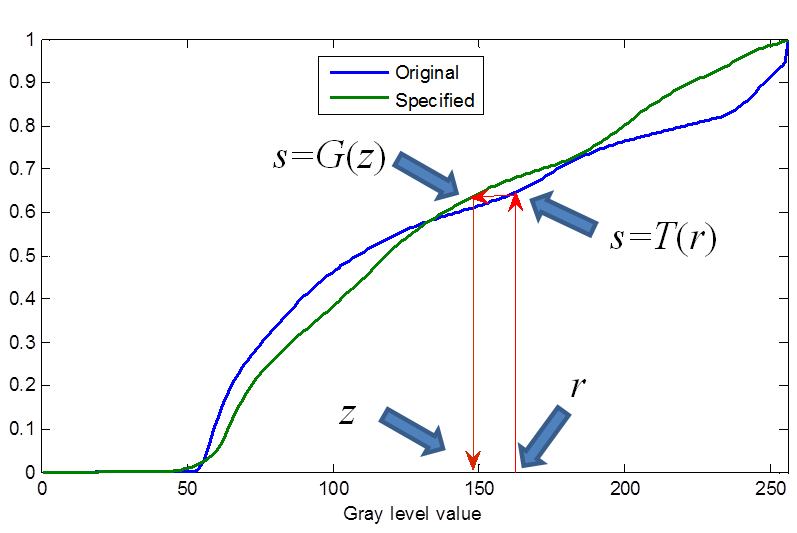
Histogram Specification

•           Histogram Specification (HS) yields an image with a PDF that follows a specified shape fZ(z) for z Ξ [0, 1].

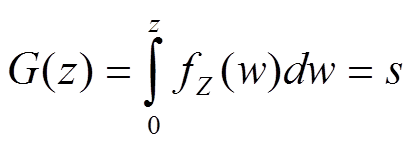•           If HE is applied to this final image, the outcome would be an image which also has a uniform PDF:

 

 

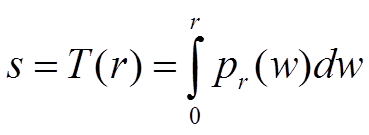Equating above expression with

 

 

 

can be used to form the transformation function that yields the specified histogram:



•           For digital normalized images with L gray level values, the implementation of histogram specification is based on the formulation of

 

 

 

 

 


 

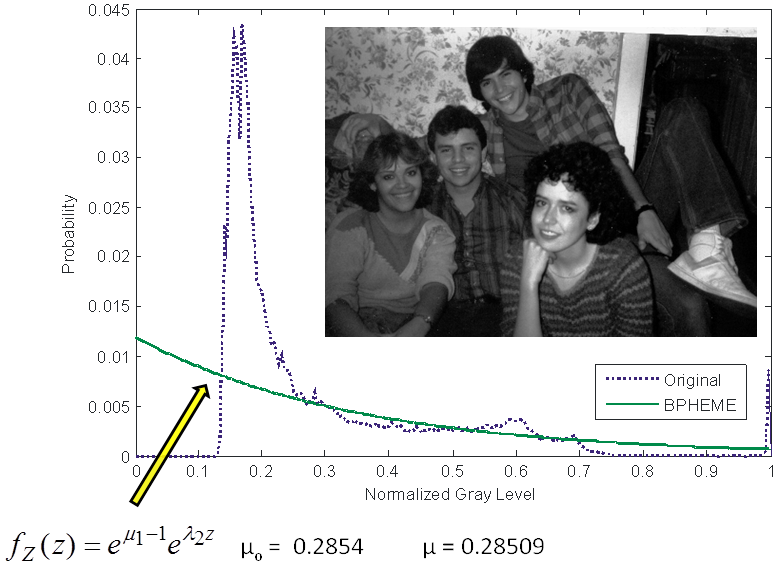
Histogram specification: BPHEME

 

C. Wang and Z. Ye, “Brightness Preserving Histogram Equalization with Maximum Entropy: a Variational Perspective,” IEEE Transactions on Consumer Electronics, Vol. 51, No. 4, pp. 1326-1334, November 2005.

 

•           The idea is to find a specified histogram fZ(z) which mean or average level of brightness is equal to the original one subject to the constraint that the entropy is maximum.

•           Mathematically the method is expressed as:

 

 

 

 

 

 

 


 A functional can be formed as:

 

 

 

 

 


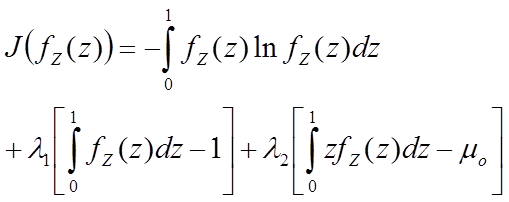
where λ1 and λ 2 are Lagrange multipliers  associated with the constraints:

 

 

 

 


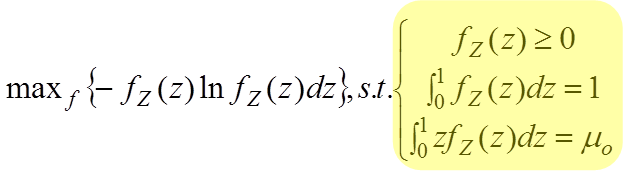
•           This is solved using calculus of variations:

 

 

 


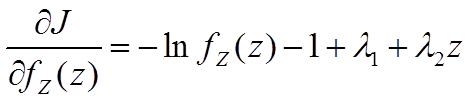
yielding :

 

Using the constraints again:

 

 



 

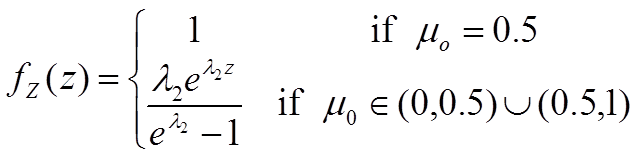
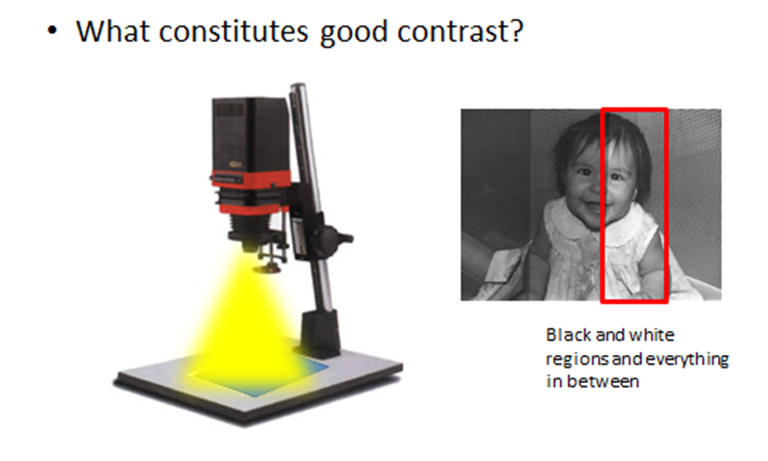
•           What can go wrong?

A photographer once said:

Photography is like painting, our media is light.

 

 

 

 

 

 

 

 


Very limited brush