136.275, Assignment No. 6
March 17, 2004
The assignment is due Wednesday, March 24 in class. Late assignments receive a mark zero.
1. Let f(x,y)= 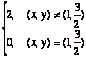 and let R = [0,2]X[0,3].
and let R = [0,2]X[0,3].
a) Draw a picture of the graph of f over the rectangle R. [1]
b)For ![]() >0, let
>0, let ![]() be the partition
of R such that on [0,2]: x0=0, x1=1–
be the partition
of R such that on [0,2]: x0=0, x1=1–![]() ,
,
x2=1+![]() and x3=2, while on [0,3]: y0=0, y1=
and x3=2, while on [0,3]: y0=0, y1=![]() –
– ![]() , y2=
, y2=![]() +
+![]() and y3=3.
and y3=3.
Draw a picture with the partition
![]() of R.
of R.
Write and calculate the double Riemann sum for f with partition ![]() and
and
with the choice of points: middle of each of the subrectangles . [6]
c) If f is integrable (which it
is) guess the value of ![]() by using
by using
part
b). Can you find ![]() by using Fubini’s
theorem. Explain. [3]
by using Fubini’s
theorem. Explain. [3]
2. Find the surface area of the portion of the paraboloid z= 4 – x2 – y2 between
the planes z=0 and z=1 . [6]
3.
Rewrite the integral
![]() as
integral in dzdydx, dy dx dz and
as
integral in dzdydx, dy dx dz and
dy dz dx. Draw a sketch of the solid over which you are integrating and of the
regions in the zy, yx and xz planes.[11]
4. Question No. 38 on page 1075 of the textbook. [9]
5.
Show that ![]() , where the
improper triple
, where the
improper triple
iterated integral is to be viewed as the limit of a triple integral over a ball, as the radius of the ball increases indefinitely. [7]
Total [ 43/42]