[10] 1. Consider the linear system
.
(a) Determine all values of a and b for which the above system has solutions.
(b) When the solution exists, can it be (write YES or NO for each of the three cases):
i) unique,
ii) one-parameter,
iii) two or more parameters?
[
8] 2. Let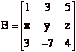 
. Given that 
= 10, find the
determinant of the following matrix:
.
[11] 3. Let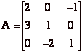 
and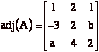 
.
(a) Find a
and b in the 
.
(b) Find 
by
using 
from (a).
[
8] 4. Let 
. Find 
by
expanding along the third column.
[10] 5. Let A
be a 
matrix,
and let B be derived from A
by multiplying row two
by –3 and adding it to row three.
(a) Find the elementary matrix E such that B = EA.
(b) Find the elementary matrix F such that A = FB.
[12] 6. A
point 
and a
line 
are given.
(a) Check that the point P is not on the line.
(b) Write the parametric equations for a line that is parallel to the given line and passes through the point P.
(c) Is the given line
parallel or perpendicular to the plane
? Explain your
reasoning.
[ 7] 7. Let u, v and w be vectors in 3-space. Indicate (by an "X") which of the following vector expressions are defined and which are undefined. If an expression is defined, indicate (by an "X") whether the expression represents a vector or a scalar.
|
vector expression |
undefined (or meaningless) |
defined (or meaningful) vector scalar |
|
(u • v) + w |
|
|
|
u • (v + w) |
|
|
|
(u ´ v) + w |
|
|
|
(u • v) • w |
|
|
|
(u ´ v) ´ w |
|
|
|
(u • v) ´ w |
|
|
|
u • (v ´ w) |
|
|
[20] 8. (a) Find two unit vectors
in 
whose dot
product with the vector (3, 4) is zero.
(b) Let S be a subset
of 
consisting
of all vectors with initial point at the origin, whose dot product with the
vector 
is zero. Find the point normal form of the plane
containing S.
(c) Find the area of the
parallelogram determined by the vectors
and 
.
(d) Find the cosine of the angle
between the vectors 
and 
.
[10] 9. (a) What does it mean to
say that the set 
is
linearly independent?
(b) Show that the vectors 
and 
are linearly
dependent.
[12] 10. Let W
be the set of all diagonal 
matrices
A with 
and
let U be the set of all polynomials of the form 
, with a
and b in R.
(a) Show that W
is a subspace of 
(vector
space of all 
matrices).
(b) Show that U
is not a subspace of 
(vector
space of all polynomials of degree less or equal to 2).
(c) Give an example of a
non-empty subset of 
that is
not a subspace of 
.
Explain your reasoning.
[12] 11. Let A be the
matrix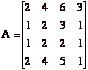 
.
(a) Find a basis for, and the dimension of, the row space of A.
(b) Find a basis for, and the dimension of, the column space of A.
(c) Find a basis for, and the dimension of, the solution space of A.