Harmonics

Consider again the waves produced by the bass clarinet and the flute. The lines in these spectra look suspiciously evenly-spaced. This is a typical property of naturally occurring waves.

Consider a guitar string. It can vibrate in a simple back-and-forth motion:

But it can also vibrate in more complex ways, where each half or third of the string is moving in the opposite direction from its neighbours:

To see tacky animated graphics of these modes of vibration, click: first mode, second mode, third mode.

Naturally occurring waves in a guitar string involve all three kinds of vibration simultaneously, and an infinite number of others.

Each mode of vibration produces a simple wave with its own frequency and amplitude:

  1. The frequency of the simple wave produced by the simplest back-and-forth motion is called the fundamental frequency.
  2. The frequency of the simple wave produced by the second mode of vibration (where the string is vibrating in halves) is twice the fundamental frequency, or exactly one octave higher.
  3. The frequency produced by the third mode (where the string is vibrating in thirds) is three times the fundamental frequency.
  4. etc.
Each of the higher-frequency simple waves is called a harmonic. In naturally occurring vibrations, there is a harmonic at each multiple of the fundamental frequency -- theoretically all the way up to infinity, though the harmonics decrease in amplitude as the frequency rises.

The spectrum of the wave produced by the guitar string would look like:

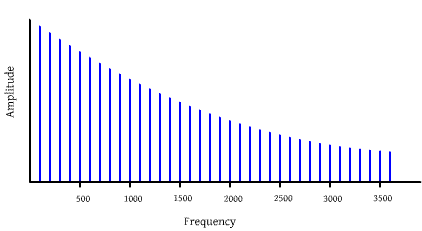
The wave produced by the vibration of the vocal cords also has this kind of structure. The wave produced by the vocal cords (before it is modified by the vocal tract) is often called the glottal wave. The fundamental frequency (the frequency of the lowest simple wave) is perceived as the pitch.

 

Next:  Resonance  | Previous:  Sound and light  | Up:  Acoustic phonetics  | Home:  Home