136.275, Assignment No. 6

March 17, 2004

The assignment is due Wednesday, March 24 in class. Late assignments receive a mark zero.

1. Let f(x,y)= 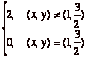and let R = [0,2]X[0,3].

a) Draw a picture of the graph of f over the rectangle R. [1]

b)For >0, let be the partition of R such that on [0,2]: x₀=0, x₁=1–,

x₂=1+ and x₃=2, while on [0,3]: y₀=0, y₁=– , y₂=+ and y₃=3.

Draw a picture with the partition of R.

Write and calculate the double Riemann sum for f with partition and

with the choice of points: middle of each of the subrectangles . [6]

c) If f is integrable (which it is) guess the value of by using

part b). Can you find by using Fubini’s theorem. Explain. [3]

2. Find the surface area of the portion of the paraboloid z= 4 – x² – y² between

the planes z=0 and z=1 . [6]

3. Rewrite the integral as integral in dzdydx, dy dx dz and

dy dz dx. Draw a sketch of the solid over which you are integrating and of the

regions in the zy, yx and xz planes.[11]

4. Question No. 38 on page 1075 of the textbook. [9]

5. Show that , where the improper triple

iterated integral is to be viewed as the limit of a triple integral over a ball, as the radius of the ball increases indefinitely. [7]

Total [ 43/42]