Lecture 6, part 2 of 2
| PLNT4610/PLNT7690
Bioinformatics Lecture 6, part 2 of 2 |
Scoring must account for those comparisons. Consider the alignment of k sequences of length n
MQPILLL
MLR-LL-
MK-ILLL
MPPVLIL
For every position
(column) in the alignment, we calculate the sum of scores, based
on the amino acid substitution matrix (eg. PAM250) using the
function
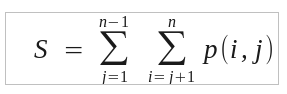
where i and j refer to all unique pairs of sequences, ignoring self comparisons, and eliminating duplicate comparisons.
The sum-of-pairs (SP)
function scores each position in the protein, that is, each
column, as the sum of the pairwise scores. For k
sequences, there are k(k-1)/2 unique pairwise
comparisons, excluding self comparisons.
For example, in column 4, the score would be
SP-score(I,-,I,V) = p(I,-) + p(I,I) + p(I,V) + p(-,I) + p(-,V) + p(I,V)
where p(a,b) is
the pairwise score of two amino acids. This function is valid
regardless of the order of sequences in the alignment.
Unlike pairwise
alignments, it is legitimate in multiple alignments to have a
match between two gap characters. By definition , p(-,-) = 0.
Although one might be tempted to score a gap as highly negative,
when two sequences match at a gap, it indicates that both
sequences have a deletion at that position, that is not shared
by other sequences.
Gaps that are conserved between two sequences represent the
conservation of a unique evolutionary event. Put another way, if
two sequences have a gap at the same position, they haven't
changed. In contrast, when two amino acids are drastically
different, that indicates a significant mutational event.
Matching gaps therefore should get a higher score than, for
example, a mismatch between two very different amino acids, such
as Proline and Lysine.
Generalizing the pairwise dynamic programming algorithm to k sequences is, in essence, doing an alignment in k dimensions. For example, an optimal alignment between k=3 sequences could be visualized in 3 dimensions:
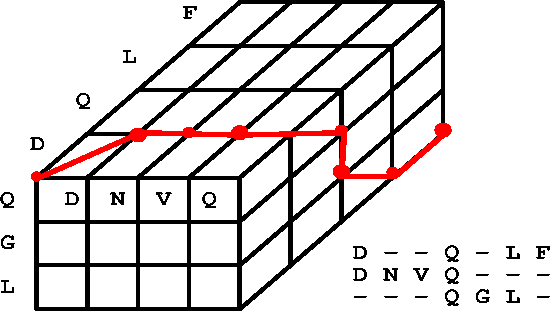
Figure 2 from Zucker [http://www.genetics.wustl.edu/bio5495/1999-course/lecture.7/]
The problem with the dynamic programming algorithm is size and speed. To start with, where k sequences of length n are compared, the storage required for the alignment matrix is O(nk). For 20 sequences of 500 amino acids each, it would require 50020 units of storage (eg. bytes).
Recall that in a pairwise comparison, for each cell in the 2-dimensional array the score was dependent on the 3 preceeding adjacent cells. In a k-dimensional array, there are 2k-1 preceeding cells. (This makes sense: for k=2 ie. a pairwise comparison, 22-1 = 3). Finally, for each column, there are k(k-1)/2 pairwise comparisons.
In summary, the time required for a truly exhaustive multiple alignment, using the most straightforward approach, is O(k22knk).
Figure from Zucker [http://www.genetics.wustl.edu/bio5495/1999-course/lecture.7/]
|
Although some methods have introduced great efficiencies that bring global dynamic programming to a level that is practical for a handful of sequences, more efficient approximate methods are needed for typical alignment problems. Probably the single most important speedup method for dynamic programming methods [Carillo and Lipman (1988) SIAM J. Appl. Math.48:1073-1082, Altschul and Lipman (1989) SIAM J. Appl. Math. 49:197-209]. This method only scales to about 8 sequences, so it is not usually practical.Optimal multiple alignments are an example of NP complete problems. NP complete problems are problems whose solutions can not be done in polynomial time. Polynomial time requires O(n c ) steps, where c is a constant. In contrast, an NP complete problem requires O(nx ) steps, where x is proportional to the size of the dataset. So, in the equation above, the real culprits are the exponential terms 2k and nk. |
 |
| interior nodes (red) - each level is an
alignment of some subset of the sequence dataset. sequences (blue) - The terminal nodes of each branch are the sequences in the alignment. |
|
As illustrated, the
sequences to be aligned are the end nodes, the "leaves" of the
tree.
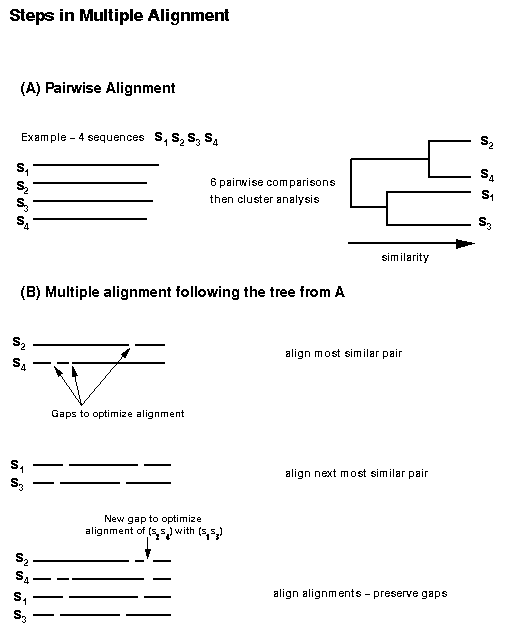
CLUSTAL ALGORITHM
| Step | Efficiency |
1. Calculate distances between all possible pairs of sequences |
O(n2) |
2. Construct a Neighbor-Joining tree from pairwise distances |
O(n) |
3. while (not all nodes on the tree have been visited) |
O(log2(n)) |
In effect,
this algorithm keeps going deeper and deeper into the tree,
clustering larger and larger groups of sequences. Clusters
(profiles) are merged, until the root of the tree is reached.
from G. Fuellen, Multiple Alignment. Complexity
International 4, 1997. URL http://journal-ci.csse.monash.edu.au/ci/vol04/mulali/mulali.html.
| EXAMPLE:
Progressive Alignment The alignment starts with the individual sequences and progresses up the tree until a final alignment is complete. |
 |
| from https://www.ncbi.nlm.nih.gov/CBBresearch/Przytycka/download/lectures/PCB_Lect05_Multip_Align.pdf |
|
| WARNING
- The guide trees produced by programs such as clustal in
step A are not
legitimate phylogenetic trees! They should never be
used for any purpose other than creating the alignment. Reason: A good phylogeny is calculated from all of the information in the multiple alignment. Because of the "once a gap, always a gap" rule, pairwise distances calculated from the final alignment may contain gaps not present in the original pairwise alignments. Thus, the original pairwise alignments would underestimate the distances across the whole tree. |
FFT-NS-1
|
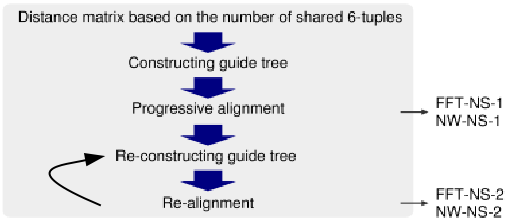 |
FFT-NS-i (2 cycles)
FFT-NS-i (up to 1000 cycles)
|
 |
| The
distances between any 2 sequences in the guide tree can be
used as a weight, which can be multiplied by the SP score
for those two sequences. For example, the distance between sequences A and C would be wA,C = wA + wC |
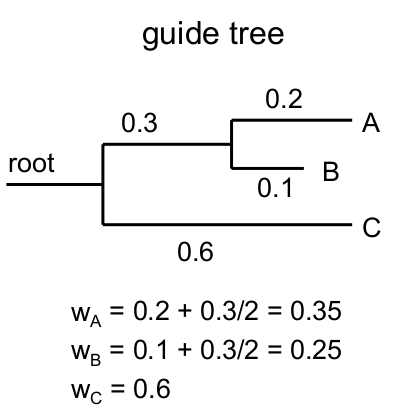 |
| We
can modify the SP function by multiplying each SP score
between two sequences i and j at any position by the
weight wij. |
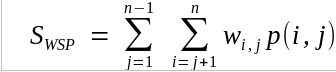 |
| pre-calculate
all pairwise alignments between each pair of sequences
to create a library of aligned sequence pairs for each aligned sequence pair in the library calculate all possible alignemts with sequence c choose the highest-scoring three-way alignment |
MAAFT implements three versions of this iterative alignment process, each optimized for different cases. As with FFT-NS-i, alignments are iterated until no further improvement is seen in the alignment score. |
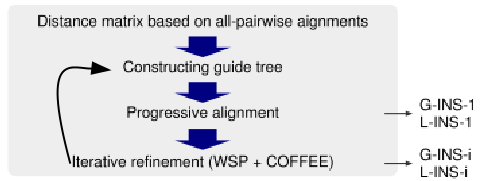 |
XXXXXXXXXXX-XXXXXXXXXXXXXXX XX-XXXXXXXXXXXXXXX-XXXXXXXX XXXXX----XXXXXXXX---XXXXXXX XXXXX-XXXXXXXXXX----XXXXXXX XXXXXXXXXXXXXXXX----XXXXXXX |
ooooooooooooooooooooooooooooooooXXXXXXXXXXX-XXXXXXXXXXXXXXX------------------ --------------------------------XX-XXXXXXXXXXXXXXX-XXXXXXXXooooooooooo------- ------------------ooooooooooooooXXXXX----XXXXXXXX---XXXXXXXooooooooooo------- --------ooooooooooooooooooooooooXXXXX-XXXXXXXXXX----XXXXXXXoooooooooooooooooo --------------------------------XXXXXXXXXXXXXXXX----XXXXXXX------------------ |
oooooooooXXX------XXXXooooooooooo---------------oooooooXXXXXooooooooooooooooo--oooooooooooooooo ---------XXXXX----XXXXoooooooooooooooooooooooooooooooooXXXXX-ooooooooooooooooooooooo----------- oooooooo-XXXXX----XXXX---------------------------------XXXXX---oooooooooo--oooooooooooo-------- ---------XXXXXX---XXXX---------------------------------XXXXX----------------------------------- ---------XXXXXXXXXXXXX---------------------------------XXXXX----------------------------------- ---------XX-------XXXX---------------------------------XXXXX----------------------------------- |
| PLNT4610/PLNT7690
Bioinformatics Lecture 6, part 2 of 2 |