Complex numbers are an amazing story in themselves.
12th Century: Bhaskara " the square of a positive number as well as that of a negative is positive. Hence the square root of a positive number is two fold, positive and negative. There is no square root of a negative number, for a negative number is not a square"
1545 Cardan, first to denote the meaningless with a symbol. Solved the quadratic x2-10x+40=0.
5(+/-)i3.873..
It was the cubic equation that made
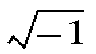a bona fide
number. x3+ax+b=0 has at least one real root. In the case of one real root, a formula called the Cardan formula will find it. In the case of three real roots the formula breaks down.
The radicals entering the formula represent imaginary numbers. Bitter dispute arose over the origin of the formula and its publication.
Bombelli used the formula on
x3=15x+4 which has real root of 4, other two roots also real.
"It was a wild thought, in the judgment of many; and I too was for a long time
of the same opinion. The whole matter seemed to rest on sophistry rather
than on truth. Yet I sought so long, until I actually proved this to be the case."
Bombelli showed the two radicals resolved to
The numbers may have been impossible, but they were not useless.
Bombelli came up with the rules we use today for operations on complex beings.
1770 Euler: Although lots of applications of complex numbers were in use stated:
"All such expressions as
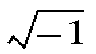.. are consequently impossible or
imaginary... and that we may truly assess that they are neither nothing, nor greater than nothing, nor less than
nothing, which necessarily constitutes them as imaginary or impossible."
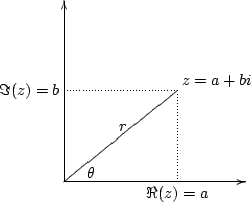
1831 Gauss: "... an objective existence can be assigned to imaginary as to negative quantities'
The thought transition was
due to
geometry, the Gauss-Argand Diagram.
