Infinity
(An excellent place to end)
Significant events:
Aristotle: Potential
infinity. Infinity that could in principle be, but in practice never
was.
Galileo: Sowed
the seeds of all that was to come (1600)
Cantor: Put infinity on a
firm logical foundation (1900)
Three kinds of
infinity: Religious, Mathematical, Physical
Truth table: Philosopher minterms
Aristotle
minterm 000
Russel
minterm 010
Cantor
minterm 111
Aquinus minterm 100
Bob
minterm X1X (don't
cares, not a philosopher anyway)
Symbol 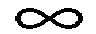 :
John Wallis around 1650 (Inventor of Integral Calculus)
:
John Wallis around 1650 (Inventor of Integral Calculus)
Early romans used a similar symbol for 1000, a big number.
Galilao: Came
closest to our
current notion of infinity.
Considered the
question whether there were
more integers than squares.
The squares are certainly less dense than integers.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 ...
Amazingly in 15something: Galilao's argument "every number has a
square, we can pair the first square with the first number, the second
with the second number, and so on. We shall never run out of squares
until we run out of numbers, since we will never run out of numbers we
will never run out of squares. Thus showing we have "as many" squares
as numbers."
"I see no other decision, but to say that all Numbers are infinite;
Squares are infinite; and that neither is the multitude of Squares less
than all Numbers, nor this greater than that; and in conclusion,
that the
Attributes of Equality, Majority, and Minority have no place in
Infinities, but only in terminate quantities"
300 years later 1880: Georg Cantor developed a precise
definition of an
infinite set.
"An infinite set, is one that can be
placed into one to one correspondence with a proper part of itself".
or
Some of the parts is equal to the
whole :)
This required a significant amount of mental and physical persistence
as it tends to go against an axiom of Euclid, where, the "whole is
greater than the part". Cantor's work around was that the axiom
did not apply to infinite quantities.
This leads immediately to seeing that the number of rational
points on a line 1 inch long are the same as the number of points on a
line of any length.
Some of Cantor's arguments are the most elegant for infinite sets.
Here is a proof that rational numbers are "equal" to the integers. That
is, can be placed in one to one correspondence with the integers.
Write the fractions with the sum of the
numerator and denominator equal to 2, i.e 1/1
Write the fractions with the sum of the
numerator and denominator equal to 3, i.e 1/2 and 2/1
Write the fractions with the sum of the
numerator and denominator equal to 4, i.e 1/3, 2/2, 3/1
etc. (eventually you get all rational
numbers)
Write them out as 1/1 1/2 2/1 1/3 2/2 3/1
... which has a one to one correspondence with the integers. Done!
Cantors proof of an infinity larger than
the counting numbers.
Consider the infinite fraction (real numbers that are not rational)
Suppose they are lined up with the counting numbers. Proof by
contradiction.
1 0.435783425708765809...
2 0.573456627669679867...
3 0.674354615645652615...
4 0.567545645789431432...
5 0.454433443466675668...
6 0.676575645648986564...
7 0.122135467619578989...
etc.
You can find another by writing a number that is different from the
above along the diagonal.
Candidate: 0.3467298.... will not show up in any list paired with the
integers as it is different than all of them.
The infinity of real numbers is
"stronger" than the infinity of the integers.
The set of of decimal fractions is non-denumerable.
Cantor demonstrated many other uncommon notions.
For example: The number of points in the plane is the same as the
number of points on a line. Pick a point on a unit square.
e.g. (0.34534543522... , 0.65453454325..)
The corresponding point on the unit line.
0.364554354354453453222... one number from each of the above shuffled.
Obviously, the reverse is a similar mapping. Establishing a one to one
correspondence.
etc. to higher dimensions! Obviously counter intuitive.
Alephzero,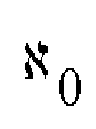 first transfinite cardinal
number, a cardinal number about
infinite sets (positive integers).
first transfinite cardinal
number, a cardinal number about
infinite sets (positive integers).
Cantor stated i) that this was the smallest transfinite number and ii)
for every transfinite number there exists a next larger transfinite
cardinal.
Cantor called the transfinite cardinal number associated with the reals
c, "the number of the continuum". He knew it was Alephsomething.
Symbolically, the continuum hypothesis is that
Alephone = c.
Gödel's and Cohen's established that the validity of the
continuum hypothesis depends on the version of set theory being used,
and is therefore undecidable
The next largest transfinite cardinal is Alephone.
A generalized version of the continuum hypothesis is 2alepha
= alepha+1, which
is also undecidable.
Ignoring the undecidability, here is a simple analog.
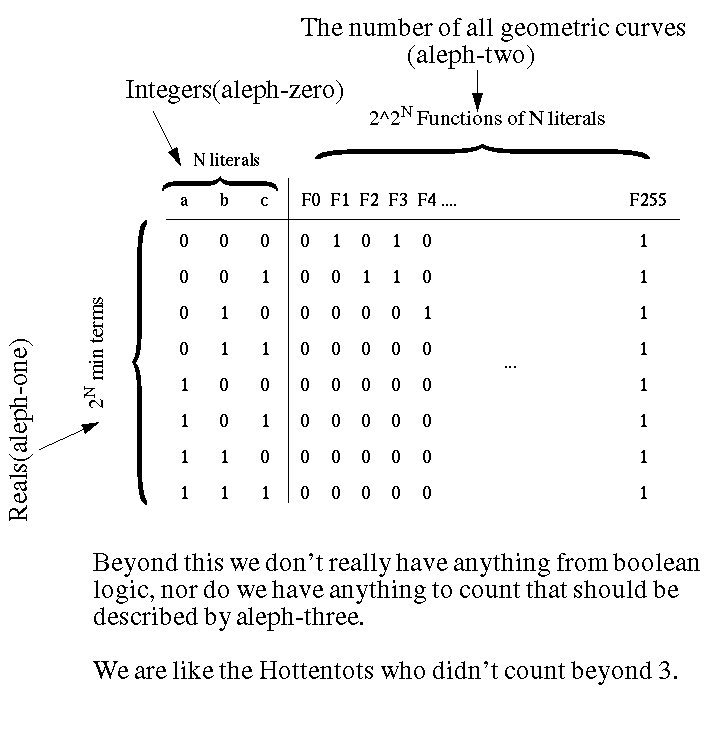
One final existence proof of Cantor's
(penultimate actually)
What do we know? We know there are Integers, Rationals, Reals. We
know there are more Reals than Integers. We know there are algebraic numbers, id est,
numbers that are solutions to algebraic equations, such as x2
= 2. We know there are numbers that are not algebraic, like
e and pi. How do these transcendental
numbers compare
with the algebraic numbers? That is the
question?
Are there more algebraic numbers like root2 or more numbers like pi?
Cantor's existence proof of transcendental numbers.
For an algebraic equation define the height h of the equation as the
sum of the magnitude of the coefficients and the equation's degree n.
This is clearly a finite number. n is clearly less that h. The
number of algebraic equations of height h = (h+1)h+1. These
can be placed in one to one correspondence with the the Integers. Each
equation of degree n can have at most n solutions. These solutions
(algebraic numbers) can be listed again in a one to one correspondence
with the Integers, and omitting duplicates is a one to one mapping.
Thus the algebraic numbers are Aleph-zero.
However the continuum c is greater that Aleph-zero. c is made up of
algebraic and transcendental, hence the transcendentals are the same as
c, or Aleph-one.
Amazingly although we only know of a handful of transcendentals, such
as e and pi. If you were to pick a real number at random from c it
would most likely with extremely high probability be transcendental.
Final Thoughts: What about numbers that are not computable?
Quiz 4: Are there more computable
numbers like 5, root2, pi, e than non computable numbers?
As it turns out the computable numbers are denumerable, id
est, countable, id est, Aleph-zero. The non computable are of the same
size as the continuum c, likely Aleph-one.
Amazingly although we only know lots of computable numbers,
such as 5, root2, e and pi. If you were to pick a real number at random
from c it
would most likely with extremely high probability be non computable.
That brings us to the
end, thank you for your time.
References:
- "Number", Tobiaz Dantzig, 4th Edition , 1954.
(Masterpiece Science Edition, 2005)
- The web of course.
- "From Zero to Infinity", Constance Reid, 1955. (50th
Anniversary Edition, 2005)
- "The Infinite Book", John D. Barrow, 2005, not as good,
but British.
- "One, Two, Three, Infinity", George Gamow, 1961
Edition, 1988 Dover.
- "Concepts of Modern Mathematics", Ian Stewart
Dover 1995 edition
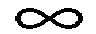 :
John Wallis around 1650 (Inventor of Integral Calculus)
:
John Wallis around 1650 (Inventor of Integral Calculus) 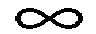 :
John Wallis around 1650 (Inventor of Integral Calculus)
:
John Wallis around 1650 (Inventor of Integral Calculus) 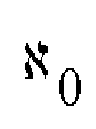 first transfinite cardinal
number, a cardinal number about
infinite sets (positive integers).
first transfinite cardinal
number, a cardinal number about
infinite sets (positive integers).