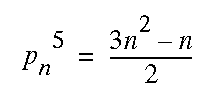Five

Another religious number, also prime.

Closely connected to Phi (fee).

Pentagonal numbers: sum of one plus every third number.

1=1
1+4 =5
1+4+7=12
1+4+7+10=22

Every number can be expressed as the sum of 5 pentagonal numbers or fewer, likely proved by Euler.

The theory of partitions concerns how many ways a number can be partitioned into the sum of its parts.

For example, 4 can be partitioned in 5 distinct ways:

4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1.

Euler's partition function p(n)

These are the same numbers that come out of the formula for the pentagonal numbers alternating between positive and negative n.

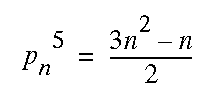
In other words: $(1-x)(1-x^2)(1-x^3) \times \cdots = 1 - x - x^2 + x^5 + x^7 - x^{12} + x^{15} - x^{22} - x^{26} + \cdots.$

While p(n) is generated by 1 over that. (coefficients of the generating power series are the values of p(n))

p(n) for n=1, 2, ..., are 1, 2, 3, 5, 7, 11, 15, 22, 30

Which is actually quite an amazing phenotype of the number 5.

Back Next