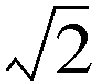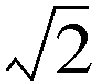First Irrational
Number Discovered.
Diagonal of a unit square.
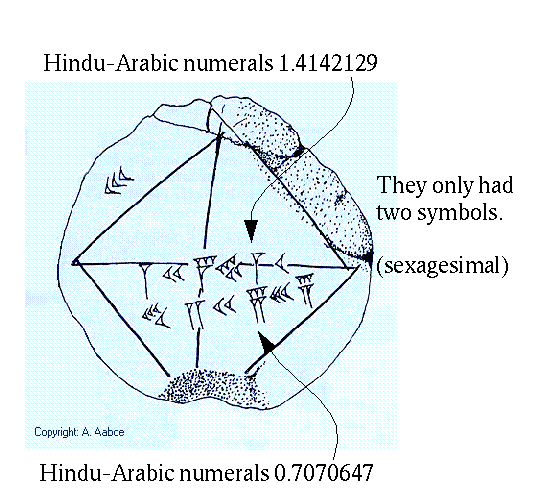
YBC: "Judging by the size and irregularity of the digits on the tablet,
this was probably a student's work, perhaps copied or maybe an
examination problem?" 2000BC !
Also found on a tablet nearby. C+ Very good Nimrod, next time,
show your work.
Of course the clay was softer then.
The accuracy: better than 1:1,000,000, so how could it have been
calculated?
Certainly not by measurement.
Perhaps by a method like Newton's Method:
First choose an
approximation to root 2, say 1.50. But 1.502= 2.25 so this
is too large.
Take
as the next approximation the average of 1.50 and 2/1.50.
Then continue this
process till you have a close enough approximation.
Perhaps they used the continued fractions of Bombelli (1572)
The first proof of irrational numbers is usually attributed to
Pythagoras, more specifically to the Pythagorean Hippasus of
Metapontum, who produced a (most likely geometrical) proof of the
irrationality of the square root of 2. (500BC) Proof by contradiction
(reductio ad absurdum).
Pythagoras did not
accept the existence of irrational numbers and so he sentenced Hippasus
to death by drowning.
Frowned upon nowadays.
Root 2 also contributed to the demise of Galois. He and others were
attempting to find analytic methods to solve general algebraic
equations. This involved the notion of rings and fields. One field of
particular interest was that of a + b root2.

Back Next