Tetration

From Wikipedia, the free encyclopedia

Tetration (also exponential map, hyperpower, power tower, super-exponentiation, and hyper4) is iterated exponentiation, the first hyper operator after exponentiation. Tetration was coined by Reuban Goodstein from tetra (four) and iteration. Tetration is used for the notation of very large numbers. Tetration follows exponentiation in the sequence:

addition

$a+b\,$
multiplication

${{a \times b = } \atop {\ }} {{\underbrace{a + \cdots + a}} \atop b}$
exponentiation

${{a^b = } \atop {\ }} {{\underbrace{a \times \cdots \times a}} \atop b}$
tetration

${\ ^{b}a = \atop {\ }} {{\underbrace{a^{a^{\cdot^{\cdot^{a}}}}}} \atop b}$

where each operation is defined by iterating the previous one.

Multiplication (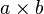 $a \times b$ ) can be thought of as B instances of A added together, and consequently exponentiation ( $a b$ ) can be thought of as B instances of A multiplied together. So a step further can be taken, and tetration ( $a \uparrow\uparrow b$ ) can be thought of as B instances of A exponentiated together.

Note that when evaluating multiple-level exponentiation, the exponentiation is done at the deepest level first (in the notation, at the highest level). In other words:

$\,\!2^{2^{2^2}} = 2^{\left(2^{\left(2^2\right)}\right)} = 2^{\left(2^4\right)} = 2^{16} = 65,\!536$

$\,\!2^{2^{2^2}}$ is not equal to $\,\! \left({\left(2^2\right)}^2\right)^2 = 256$

NEXT BACK