Density Functional Calculations on Actinide Compounds
H. Georg Schreckenbach
Department
of Chemistry
University of Manitoba
Winnipeg, MB, R3T 2N2, Canada
schrecke@cc.umanitoba.ca
This article appeared first in the March 2001 Newsletter of the CCP1, CLRC Daresbury Laboratory, Warrington, UK.
During my postdoc at
Los Alamos National Laboratory (1997-2000),
I have mainly worked in the area of theoretical actinide chemistry. This article
aims at giving a short, personal summary of some of the results. In doing so, it
is hoped that it may give an idea of the kinds of problems that can be studied to
date, and of some of the challenges that are still to be met.
1. Introduction, Background, Motivation
Theoretical actinide chemistry has been described as "a challenge to applied quantum chemistry." [1] A decade later, the challenge remains, despite considerable progress in the theoretical methods, computer programs and computer hardware. Indeed, the reliable description of the actinide elements and their compounds is one of the Grand Challenge areas for modern computational quantum chemistry.
Why should chemical research focus on actinide chemistry? Pressing environmental issues are related to actinide compounds. Numerous contaminated sites worldwide are a legacy of the Cold War and, to a lesser degree, of the peaceful use of atomic energy. While the massive cleanup of such sites is foremost an engineering problem, there is also a need for chemistry to provide reliable data on solution species that are present in ground water or storage tanks, or to design novel extraction compounds. In addition, the nuclear waste storage problem is all but solved. Again, chemistry must provide data about the behavior of actinides enclosed in glasses or in other storage facilities.
Why should theoretical chemists pursue this area of research? Besides fundamental interest [2], there is a strong practical incentive for the theoretical study of actinide complexes. Practical interest is primarily due to the radioactivity of the actinide elements and the extreme experimental difficulties arising thereof. This leaves room for theory to provide useful data to augment and enhance experimental studies.
What are the main challenges? First, the actinide elements
comprise the heaviest part of the periodic table. Consequently, there are very
many electrons that have to be dealt with, most of them occupying inert core
shells. Thus, calculations on actinide systems are inherently very large.
Second, scalar and often also spin-orbit relativistic effects have to be
included for even a qualitative understanding of the f-block (lanthanide and
actinide) chemistry [5]. Third, correlation effects
resulting from the interaction between the electrons are at least equally
important. Fourth, the 5f, 6d, 7s, and 6p orbitals are comparatively
close in energy and spatial extent and can all participate in bonding
[6]. Due to the presence of the 5f shells, there are typically
a large number of low-lying, near-degenerate states that are close in energy to
the ground state. This makes it difficult to achieve convergence in the
self-consistent solution of the quantum-mechanical equations or to describe
excited states. For open-shell systems, this may furthermore lead to complicated
spin-orbit and multiplet effects.
2. Cis- and Trans Uranyl: The [UO2X4]2- System (X = OH, F, Cl)
Figure 1. UO2F42-, UO2Cl42-, and UO2(OH)42-. Optimized (DFT-B3LYP-ECP) minimum energy structures ("trans uranyl", upper row) and stable conformers with a "cis uranyl" structure (lower row) [6].
In the higher oxidation states of the actinide metal (AnV, AnVI; An = U, Np, Pu), the very stable actinyl unit AnO2n+ (n = 1, 2) is usually formed [7]. Experimentally, it is always found that the AnO2 unit is linear or near-linear [7].
We have studied f0 uranyl (VI) systems including UO2F42-, UO2Cl42-, and UO2(OH)42- [6]. As shown in Figure 1, the ground state structures is, in every case, one with a linear arrangement of the uranyl unit as one would expect ("trans-uranyl"; upper row of the figure). However, we were also able to characterize stable conformers (local minima on the potential energy surface) that possess a bent uranyl unit, Figure 1 ("cis-uranyl"; lower row). The cis-trans energy separation appears to be inversly proprotional to the uranyl bond strength. A weaker uranyl bond destabilizes the trans- ground state, and makes the cis-conformer more readily accessible [6].
The newly found cis-structures may play a role in ligand exchange processes in
the uranyl (VI) tetrahydroxide. Clark et al. [8]
presented experimental evidence for a rapid uranyl oxo ligand
exchange in highly alkaline solutions. On the theoretical side, we have proposed
[9] a ligand exchange mechanism that involves pseudo-rotation and a
"cis-uranyl" structure as a stable intermediate, Figure 2.
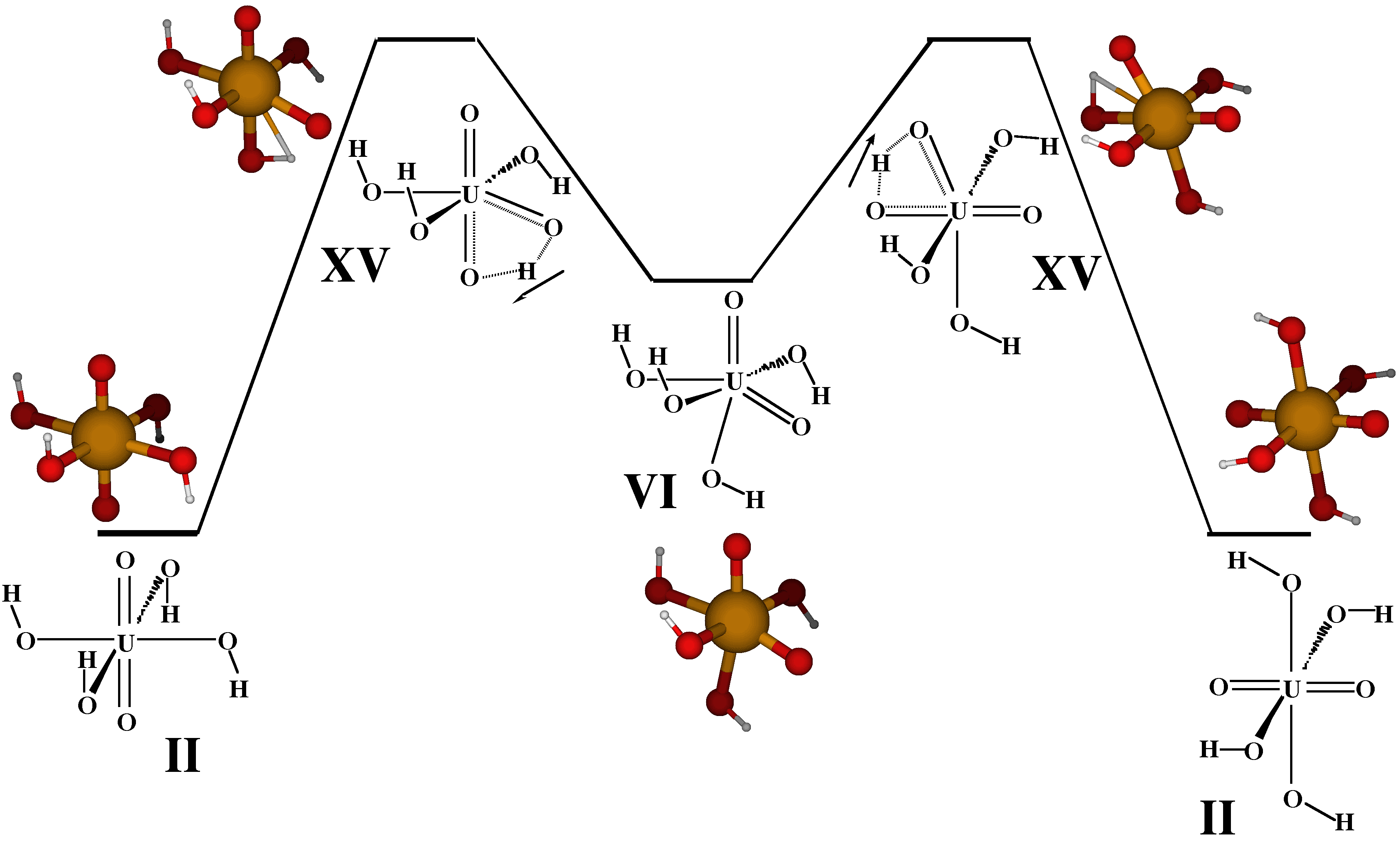
The calculated barrier (37.5 kcal/mol, Figure 2) is much higher than the experimentally obtained [8] estimate of 9.8(0.7) kcal/mol. There are various possible reasons for this discrepancy:
- Our calculated mechanism, Figure 2, refers to the gas phase. Explicit inclusion of one solvent (H2O) molecule lowers the barrier by about 6 kcal/mol. Adding the effects of the remainder of the solvent by means of an electrostatic solvation model yields a reduction by a further 5 kcal/mol [10].
- The experimental mechanism is unknown but could be different. It could, for instance, include dissociation and association steps instead of the pseudorotation. In addition, it has been found experimentally that both, the uranyl tetrahydroxide [UO2(OH)4]2- and the pentahydroxide [UO2(OH)5]3- are present in solution [8].
- Shortcomings of the theoretical model (the particular choice of ECP, approximate DFT, electrostatic solvation model) cannot be ruled out.
To the best of our knowledge, this study [9] may be the first
one where transition states have been fully characterized for an actinide molecule.
3. Actinide Chemistry in Aqueous Solution: [AnO2(H2O)5]n+ (An = U, Np, Pu; n = 1, 2)
Water is an ubiquitous solvent for actinides in the environment, in storage tanks, or in repositories. Thus, complexes of the early actinides U, Np, Pu with water have received considerable attention recently (see, for instance, [11], [12], [13] for some theoretical papers.)
We have studied the structures and vibrational frequencies of the An(V) and An(VI) complexes [AnO2(H2O)5]n+ (An = U, Np, Pu; n = 1, 2) [14]. Furthermore, reactivity and energetics were studied. The following is a brief summary of the major results; more details can be found in the original paper [14] or online (pdf document).
- Calculated bond lengths and frequencies were compared to experiment. As has been found before for various other systems, the actinyl bond length is accurately predicted whereas the equatorial bond length is overestimated.
- Experimental trends in the actinyl stretching frequency along the series have been reproduced, Figure 3. The trend along the actinide series (decrease of the stretching frequencies, Figure 3) has been related to the decrease in size of the 5f orbitals as the atomic number increases.

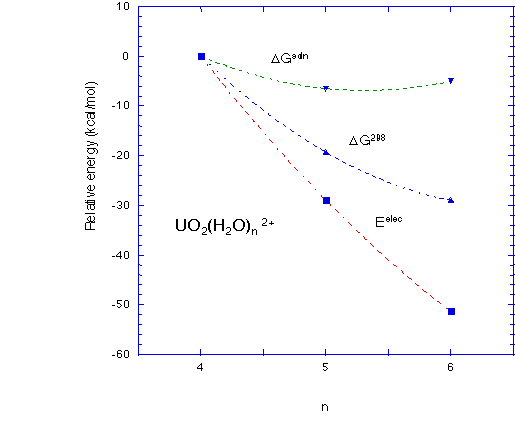
- For the uranyl system, the equatorial coordination number is predicted to be 5 (5 waters in the first coordination sphere), in accordance to experiment, but only if solvation and thermodynamic effects are included, Figure 4.
- Multiplet and spin-orbit effects have been estimated. They become important for the calculation of reduction potentials.
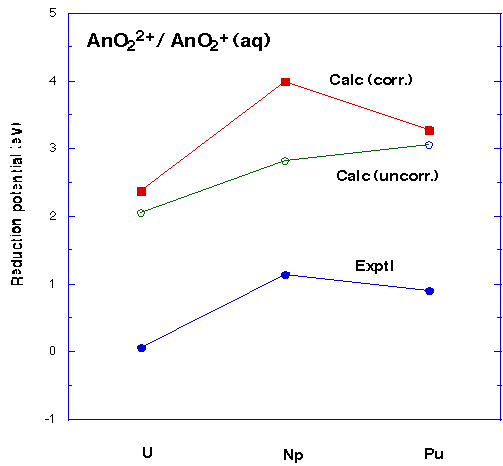
- The relative [AnO2(H2O)5]2+ / [AnO2(H2O)5]1+ reduction potential along the series An = U, Np, Pu is predicted accurately after all of correlation (by means of DFT), solvation, thermodynamic effects, multiplet effects, and spin-orbit effects have been accounted for, Figure 5.
- The absolute reduction potential shows a systematic error of some 2 - 3 eV, Figure 5. This may be due to the choice of ECP.
4. Actinide Extraction Chemistry: Actinyl Crown Ether Complexes
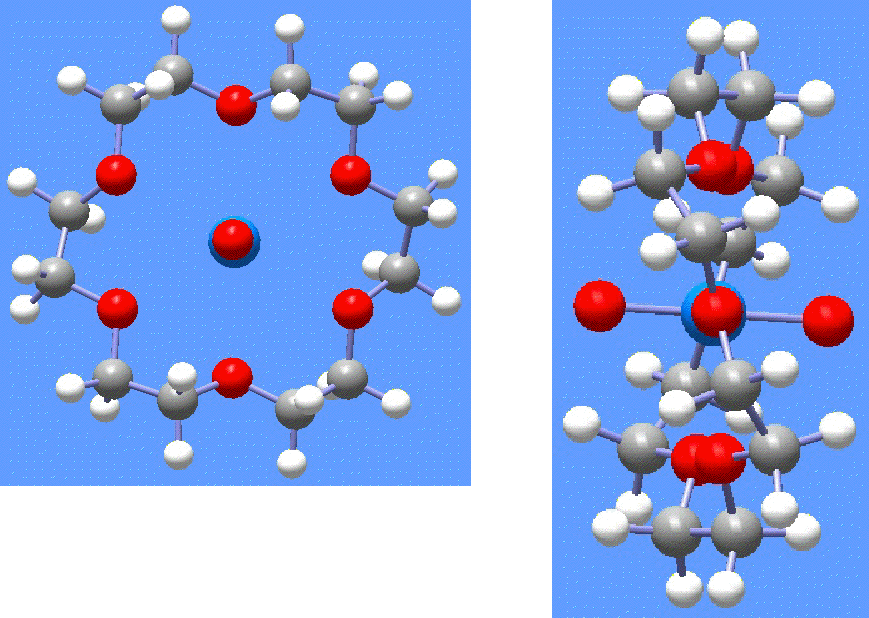
Figure 6. Optimized structure (DFT-B3LYP-ECP calculations) for the [NpO2(18-crown-6)]1+ complex [15], [16]. The top view (left) shows the encapsulation of the linear O-Np-O unit.
Clark et al. [17] recently reported the synthesis of the NpO2+ ion encapsulated by the 18-crown-6 ligand. The system was characterized crystallographically as its perchlorate salt. Further, some vibrational spectroscopy and other experimental data is available. While the uranium (VI) species, [UO2(18-crown-6)]2+, had been known and characterized previously, this is the first example of a transuranic crown ether inclusion complex.
Motivated by this synthetic accomplishment and the prospect of very similar chemistry
involving plutonium, we have undertaken theoretical studies of a series of
actinyl inclusion complexes [15], [16].
The techniques that had been successfully applied to the actinyl water complexes
[14], section 3, have been extended to actinyl crown ether
inclusion complexes [AnO2(18-crown-6)](1+,2+) where An = U, Np, Pu.
Thus, we have studied the structures (Figure 6), vibrational frequencies, solvation
properties, electronic structure, and redox potentials for these systems
[15], [16]. Some more details can be found
here (pdf document).
5. NMR Studies
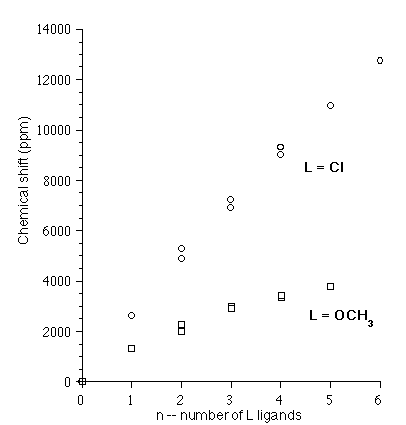
We have initiated an extensive theoretical study that is aiming at extending relativistic DFT-NMR calculations [18] to the heaviest part of the periodic table, the actinides. We have chosen diamagnetic (i.e. formally f0) uranium compounds as a representative example [19], [20], [21], [22]. Systems studied so far include uranyl complexes with various equatorial ligands ([UO2(H2O)5]2+, [UO2(CO3)3]4-, [UO2L4]2-, L = F, Cl, Br, I, OH [10], [21], [22]), UF6 [21] - the only actinide case where an entire chemical shift tensor is known experimentally [23] - and inorganic UF6 derivatives UF6-nCln (n=0-6) [20], [21], [22], organometallic UF6 derivatives UF6-n(OCH3)n (n=0-5) [20], [22], as well as uranium (VI) hexahalides UX6, X = F, Cl, Br, I [10].A proper description of relativity is crucial, and we find that relativistic effects have to be included. For ligand NMR, spin-orbit relativistic effects can, in principle, be neglected in some cases (such as the 19F NMR in UF6 und UF6 derivatives UF6-nLn, L = Cl, OCH3 and n=0-6), while it is the dominating factor in other cases, notably the 1H (proton) NMR. The mechanism for these spin-orbit chemical shifts is, by now, well understood [24]. For the metal (235U) NMR, spin-orbit effects cannot be neglected. Furthermore, the older Pauli approach to relativity appears to be at or beyond its limit in this case, and modern, stable methods such as ZORA (the zeroth order regular approximation for relativistic effects [25]) are required.
We have compared calculated ligand NMR shieldings and chemical shifts to experiment. We find moderate to excellent agreement between the calculations and the available experimental data. [21], [22]. Possible error sources have been discussed. They include the - approximate - XC functional of DFT, solvation effects (neglected in the calculations), effects of the optimized geometries and systematic errors in the calculated NMR of the reference compounds.
Furthermore, we have attempted to predict the 235U chemical shifts. Experimental NMR chemical shifts are not knwon for uranium or for any other actinide nucleus. For instance, plutonium (239Pu) is about the only spin-1/2 nucleus in the entire periodic table that has not been observed by NMR. This failure is due to a generally unfavorable signal-to noise ratio combined with large chemical shift ranges and the radioactivity of the actinides and the experimental difficulties arising thereof.
It is hoped that the present calculations [10],
[19], [20], [21],
[22]
might help to guide future experiments, by narrowing down the chemical shift range
that has to be scanned for a signal. The total chemical shift range is rather
large indeed: We predict a chemical shift range of about 36,000 ppm for
some 27 compounds studied [10], [22].
Some examples of calculated 235U NMR are summarized in
Figure 7.
6. Summary
We have, in the preceeding sections, tried to give a flavor for the kind of studies that have been performed on actinide systems. By doing so, it is hoped that we were able to give a feel for the scope and breadth of problems that have become accessible recently. Thus, we can now study a wide array of properties ranging from structures and geometries (sections 2, 3 and 4) to vibrational (sections 3 and 4) and NMR spectroscopy (section 5), from conformational studies (section 2) to reactivity (sections 3), from redox potentials and thermodynamic stability (sections 3 and 4) to excited states (not discussed here). The speed and accuracy of computers and methods has reached a point where we can, for the first time, tackle systems that are relevant, for instance, for the clean-up of contaminated sites. (Examples shown here include the water and crown ether complexes.)As has been pointed out in the introduction already, the theoretical study of actinide complexes is, however, far from being a routine area of applied quantum chemistry. A non-exhaustive list of unsolved problems and open questions might look as follows. Most of these points are, of course, not unique to the actinides although they might be more pronounced here.
- As any practitioner in the field will know, it is notoriously difficult to achieve convergence in either the self-consistent equations or geometry optimizations. This is principally due to the large number of degenerate or near-degenerate states that are formed by the metal-based 5f orbitals. As a consequence, it is a more severe problem for open shell systems than for formally f0 complexes.
- The lack of reliable experimental gas phase data for theses species makes it difficult to systematically benchmark (DFT-) methods with respect to their accuracy. Further work is needed to establish the accuracy of the different levels of approximation for both, relativity and correlation, and to establish a routine protocol for applications to practical chemical problems.
- The proper treatment of spin-orbit and multiplet effects within DFT is not fully solved. While such effects can normally be neglected for properties such as structures and vibrational frequencies, they are crucial for energetics and related properties. (See, for instance, Figure 5.)
- Further work is needed to establish solvation models that are accurate and reliable but, at the same time, computationally feasible.
- Despite considerable progress, calculations on actinide systems are still demanding for the computational ressources. Thus, this is an area that will strongly benefit from further developments in areas such as parallel computing, commodity computer clusters, or linear scaling methods.
It appears that actinide compounds will continue to present a formidable challenge to theoretical calculations at the density functional as well as Hartree-Fock and post-HF levels. This is because relativity, electron correlation, multiplet effects from electron-electron interactions, spin-orbit effects and medium effects of the surrounding solvent all play improtant roles in determining the electronic properties of these systems [6].
Acknowledgment
A sizeable part of the work presented here has been performed in close collaboration with P. Jeffrey Hay and Richard L. Martin, Los Alamos, but even the parts that did not involve direct cooperation have benefitted from their input and encouragement. I would further like to acknowledge the close and fruitful cooperation with variuos experimental researchers at Los Alamos. Most of this work has been supported under the Laboratory Directed Research and Development funding scheme at Los Alamos under the auspices of the US Department of Energy (Grant W-7405-ENG-36) as well as through the Seaborg Institute for Transactinium Sciences at Los Alamos. This article appeared first in the March 2001 Newsletter of the CCP1, CLRC Daresbury Laboratory, Warrington, UK.References
- Pepper, M.; Bursten, B. E. J. Am. Chem. Soc. 1990, 112, 7803.
- The actinide block, the lowest part of the periodic table, stands out among the elements: It is practically only here that f-orbitals participate in chemical bonding. This leads to interesting new bonding schemes and to compounds that have no analogue elsewhere in the periodic table. For instance, sandwich compounds involving the planar C8H82- ligand [3], [4], are not known for transition metals or main group elements.
- Streitwieser, A.; Müller-Westhof, U. J. Am. Chem. Soc. 1968, 90, 7364.
- Streitwieser, A. Inorg. Chim. Acta 1984, 94, 171.
- Pyykkö, P. Chem. Rev. 1988, 88, 563.
- Schreckenbach, G.; Hay, P. J.; Martin, R. L. J. Comput. Chem. 1999, 20, 70.
- Denning, R. G. Struct. Bonding (Berl.) 1992, 79, 215.
- Clark, D. L. et al. Inorg. Chem. 1999, 38, 1456.
- Schreckenbach, G.; Hay, P. J.; Martin, R. L. Inorg. Chem. 1998, 17, 4442.
- Schreckenbach, G. unpublished results.
- Spencer, S et al. J. Phys. Chem. A 1999, 103, 347.
- Blaudeau, J. P. et al. Chem. Phys. Lett. 1999, 310, 347.
- Tsushima, S.; Yang, T.; Suzuki, A. Chem. Phys. Lett. 2001, 334, 365.
- Hay, P. J.; Martin, R. L.; Schreckenbach, G. J. Phys. Chem. A 2000, 104, 6259.
- Martin, R. L.; Hay, P. J.; Schreckenbach, G. in preparation.
- Martin, R. L.; Hay, P. J.; Schreckenbach in: Pilay, K. K. S.; Kim, K. C.(Eds.), "Plutonium Futures - The Science: Topical Conference on Plutonium and Actinides" AIP Conference Proceedings 532; American Institute of Physics, 2000, p. 392-394.
- Clark, D. L. et al. Angew. Chemie Int. Engl. 1998, 37, 164.
- Schreckenbach, G.; Ziegler, T. Theor. Chem. Acc. 1998, 99, 71.
- Schreckenbach, G.; Wolff, S. K.; Ziegler, T. in: Facelli, J. C.; de Dios A. C. (Eds.), "Modelling NMR Chemical Shifts: Gaining Insight into Structure and Environment" ACS Symposium Series 732; American Chemical Society, 1999, p. 101-114.
- Schreckenbach, G. Inorg. Chem. 2000, 39, 1265.
- Schreckenbach, G.; Wolff, S. K.; Ziegler, T. J. Phys. Chem. A. 2000, 104, 8244.
- Schreckenbach, G. J. Am. Chem. Soc., submitted.
- Zeer, E. P.; Falaleev, O. V.; Zobov, V. E. Chem. Phys. Lett. 1983 100, 24.
- Kaupp, M. et al. Chem. Eur. J. 1998, 4, 118.
- Wolff, S. K.; Ziegler, T.; van Lenthe, E.; Baerends, E. J. J. Chem. Phys. 1999, 110, 7689.
Back to Homepage
Back to Research Interests
© Copyright Georg Schreckenbach, 2001 - 2005