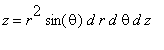> restart:

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

Consider the transformation from cartesian to polar coordinates in two dimensions

> x:=(r,theta)->r *cos(theta);

> y:=(r,theta)->r*sin(theta);

Define the jacobian of the transformation 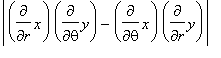i.e. determinant of partial derivatives

> j:=jacobian([x(r,theta),y(r,theta)],[r,theta]);

> detj:=det(j);

> detj:=simplify(%);

The element of area in cartesian coordinates is dA=dxdy and in polar coordinates dA=rdrd

The relationship between them is just dxdy=

Consider cylindrical polar coordinates:

> x:=(r,theta,z)->r*cos(theta);

> y:=(r,theta,z)->r*sin(theta);

> z:=(r,theta,z)->z;

> j:=jacobian([x(r,theta,z),y(r,theta,z),z(r,theta,z)],[r,theta,z]);

> detj:=det(j);

> detj:=simplify(%);

Hence the element of volume dV=dx dy dz = |J|

Spherical Coordinates

> x:=(r,theta,phi)->r*sin(theta)*cos(phi);

> y:=(r,theta,phi)->r*sin(theta)*sin(phi);

> z:=(r,theta,phi)->r*cos(theta);

> j:=jacobian([x(r,theta,phi),y(r,theta,phi),z(r,theta,phi)],[r,theta,phi]);

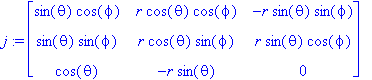
> detj:=det(j);

> detj:=simplify(%);

Hence the element of volume dV=dx dy dz = |J|