Consider expanding a function of two variables in a power series about the point x=a,y=b mtaylor(f(x,y),[x=a,y=b],3);

Example: Expand F(x,y)= sin(x) cos(y) about x=y=0

Calculate the first few partial derivatives

> F:=sin(x)*cos(y);

> Fx:=diff(F,x);

> Fy:=diff(F,y);

> Fxx:=diff(F,x,x);

> Fxy:=diff(F,y,x);

> Fyy:=diff(F,y,y);

> Fxxx:=diff(F,x,x,x);

> Fxxy:=diff(F,y,x,x);

> Fxyy:=diff(F,y,y,x);

> Fyyy:=diff(F,y,y,y);

All of the above are evaluated at x=0,y=0

> mtaylor(F,[x,y],4);

NOTE:

In the case of a single variable, the Taylor series has the form

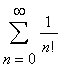
f(x) = 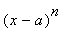= 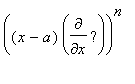f (a)

In the case of two variables it can be written as

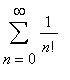
f(x,y) = 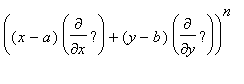f(a,b)