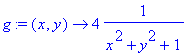
> restart;

Define a surface and plot it

> g:=(x,y)->4/(x^2+y^2+1);

> plotg:=plot3d(g(x,y),x=-2..2,y=-2..2,axes=boxed):

> with(plots): display(plotg);

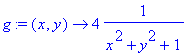
Warning, the name changecoords has been redefined

Find the first partial derivatives which give the slope of tangents in the x and y directions

> gx:=diff(g(x,y),x);

> gy:=diff(g(x,y),y);

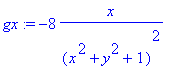
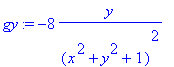
Consider the point (1/2,1,16/9 ) on this surface

> with(plottools): place:=pointplot3d([1/2,1,16/9],symbol=BOX,color=red):

> display([plotg,place]);

Find the tangent slopes at the point (1/2,1,16/9)

> slox:=evalf(subs(x=1/2,y=1,gx));

> sloy:=evalf(subs(x=1/2,y=1,gy));

The equation of the tangent plane at this point is

> z:=(x,y)->16/9 +slox*(x-1/2.)+sloy*(y-1);

Plot the surface, tangent plabe and point

> plotz:=plot3d(z(x,y),x=-2..2,y=-2..2):

> display([plotg,plotz,place]);

>