Resonance

Some examples of resonance:

• a standing wave on a skipping rope.
• the note you get when you blow into a half-full beer bottle
• the vibrations in the sounding board of a violin
• a swing swinging higher when you push it just right, or you "pump" just right while you're sitting in it

Resonance in a half-open tube

You can get a standing wave in a half-open tube if the area of high-pressure reaches the open end at exactly the same time the closed end returns to normal pressure.

When this happens, the "reflected" waves travelling back from the open end will exactly coincide with the waves travelling forward from the closed end and they will reinforce each other. The tube will resonate. (At a non-preferred frequency the backward-moving waves will sometimes reinforce, sometimes cancel out, the forward-moving waves, and you won't get a standing wave.)

The preferred frequencies for a half-open tube will be all those frequencies (call them X) such that: the length of the tube is 1/4 the wavelength of X, or the length of the tube is 3/4 the wavelength of X, or the length of the tube is 5/4 the wavelength of X, and so on. (This is often called the "odd-quarters law".) This means the second resonating frequency will be three times higher than the first, the next will be five times higher, and so on.

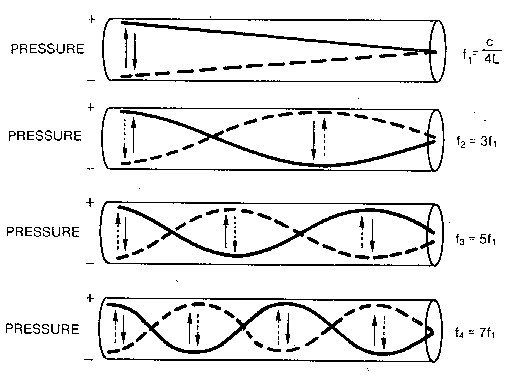
For a half-open tube that is 17 cm long (a typical length for an adult male's vocal tract), the preferred frequencies are 500 Hz, 1500 Hz, 2500 Hz, 3500 Hz, and so on.

We often diagram the frequency response curve of a tube. This shows for each frequency how much a tube would resonate if you gave it vibrations at that frequency. The frequency response curve for a 17 cm long vocal tract held in neutral position (i.e., the position for schwa) looks like: