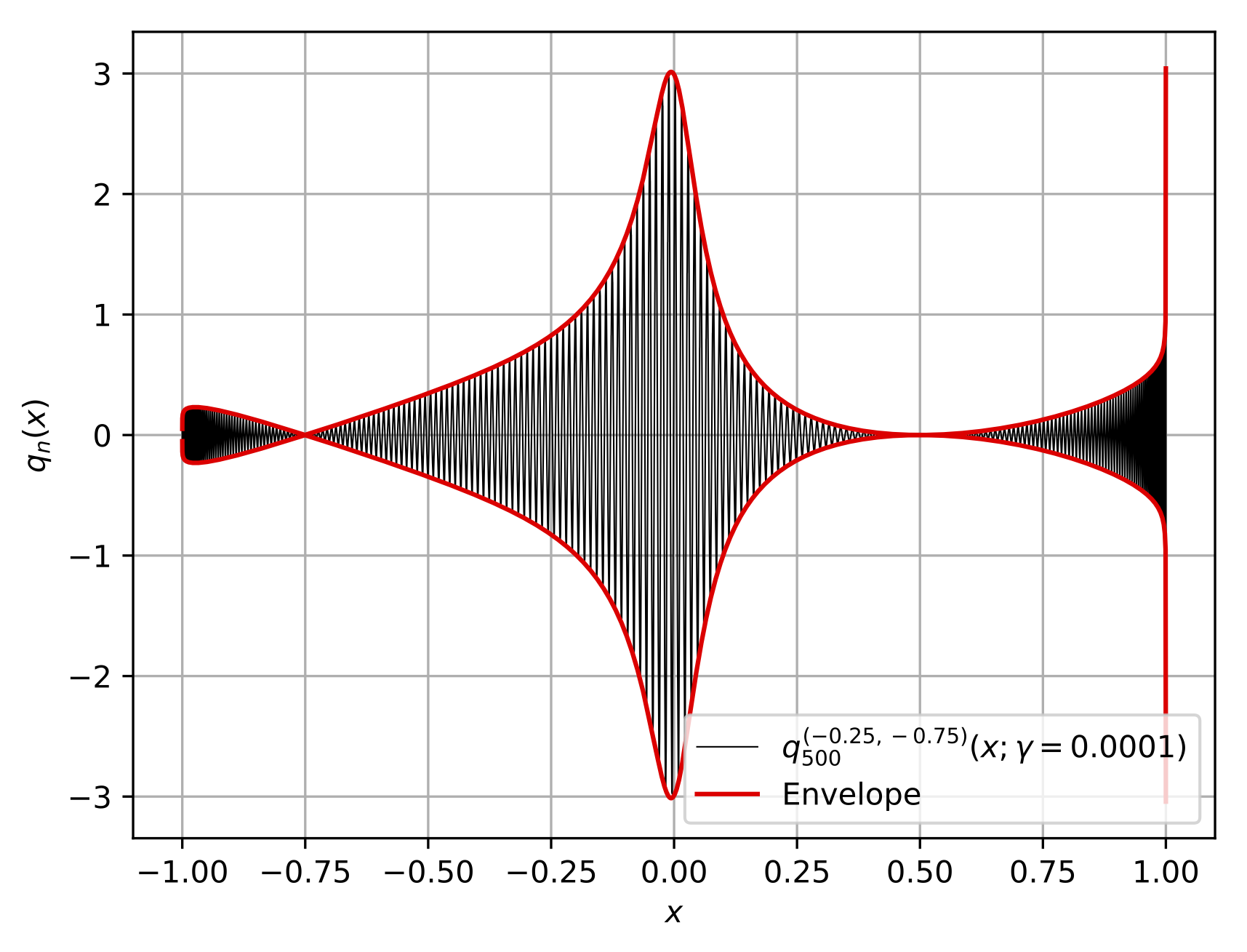
Orthogonal polynomials are a central object in numerical analysis. They enable \(L^2\) polynomial approximation theory and spectral methods for solving differential and integral equations. Classical orthogonal polynomials are special because they are the only orthogonal polynomials whose derivatives are also orthogonal polynomials. In my paper with Timon S. Gutleb and Sheehan Olver, we discuss algorithms for polynomial and rational measure modifications. These lead naturally to infinite banded matrix factorizations for the connection coefficients between the original and modified polynomials. The polynomial modifications result in computable Cholesky and \(QR\) factorizations, while the rational modifications require approximations to noncomputable factorizations such as reverse Cholesky and \(QL\). Along the way, we also discovered a certain class of modified classical weights that allow for banded differentiation matrices, generalizing the property of classical orthogonal polynomials. To the right, we see a modified Jacobi polynomial plotted in quasi-linear complexity.

Every physical shape resonates at a particular set of frequencies with distinct amplitudes. These amplitudes are known as harmonics, and the spherical setting has a rich history. Every square integrable function defined on the surface of a sphere can be decomposed into a spherical harmonic expansion, those particular vibrating modes on the sphere. Transforming a set of function samples to expansion coefficients and back is a problem of significant interest to numerical analysts and applied mathematicians alike. Why do we care? It turns out that weather forecasting is sensitive to the underlying geometry of the surface of the Earth, and a sphere is a good approximation for use in global numerical weather prediction. Astrophysicists interested in studying the Big Bang scan the skies for cosmic background radiation; plainly, they are looking for the very first light emitted by the universe. This analysis is spherical in nature because of the angular coordinates we assign every outward direction, and just the right information can be gleaned from the data represented in spherical harmonic expansions. My contribution is to significantly increase the practicality of spherical harmonic transforms, reducing previously published pre-computation times by orders of magnitude, and by proving asymptotically optimal complexity and stability of the transforms. The paper and preprint are available online and the software is open source and also freely available. To the right is an image describing a skeletonization procedure that is responsible for the increased performance.

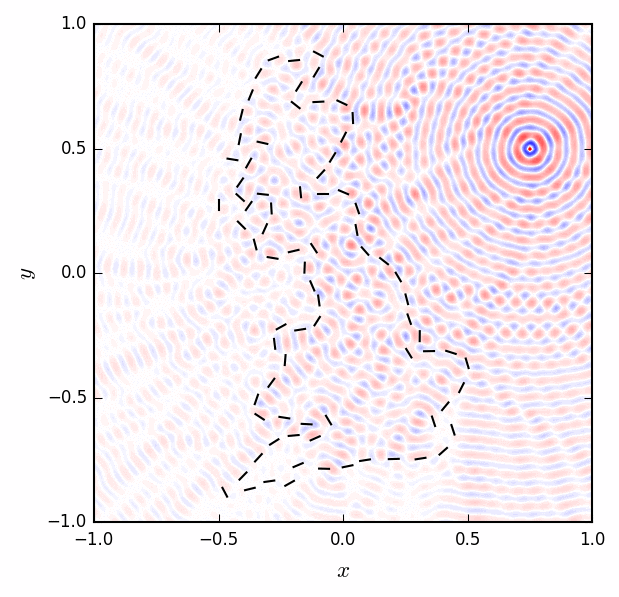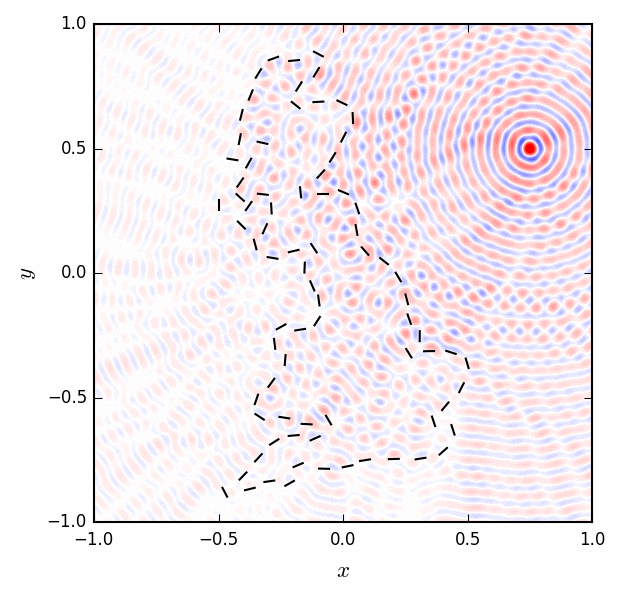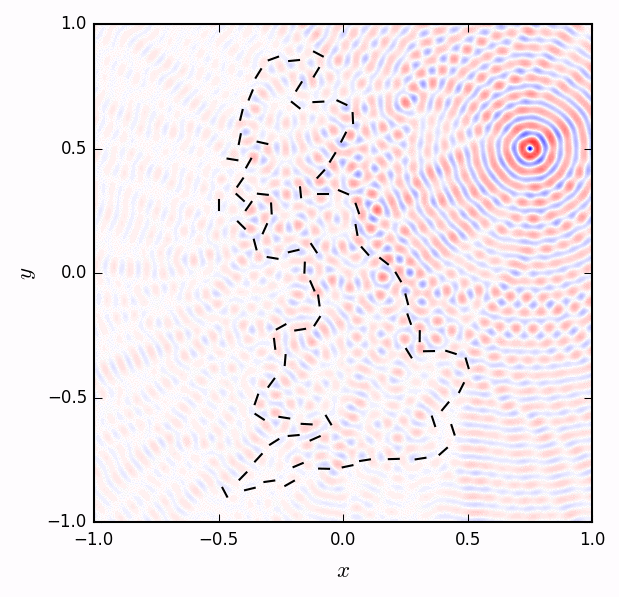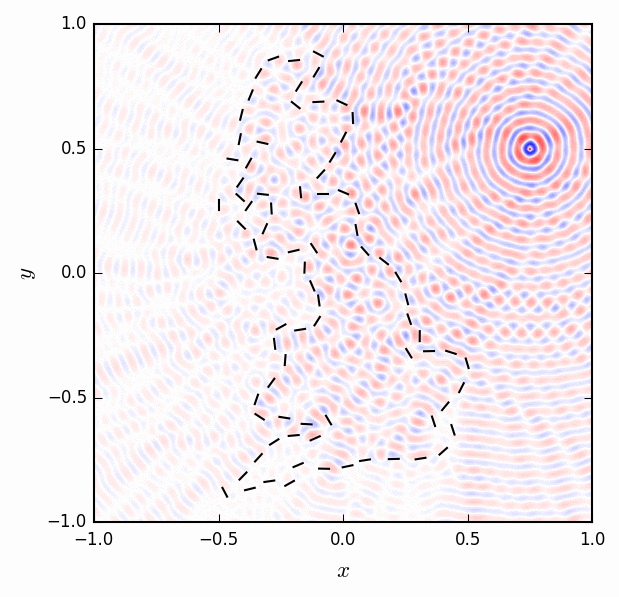
Partial differential equations in two and three spatial dimensions are solved in closed-form by integrals over fundamental solutions (historically traced back to Green's functions). These integrals are convenient because they give global solutions to the PDEs based on local data of a reduced dimension. Determining the local data requires the solution of singular integral equations. If we consider the Helmholtz equation, for example, the local data represent jumps in the wave along prescribed boundaries. In my paper with Sheehan Olver, we solve for the jumps by splitting the solution into an incoming wave and an outgoing wave that sum to satisfy the boundary conditions. The solution is computed to high accuracy by adapting a spectral method for linear ordinary differential equations to singular integral equations. Why do we care? The Helmholtz equation, and its direct current (DC) limit the Laplace equation, describe the scattering of acoustic and electromagnetic waves; they are important for designing everything from opera houses to WiFi routers to analyzing radar and seismic images. To the right, electromagnetic radiation emanating from a point source is scattered by an outline of the isle of Great Britain.

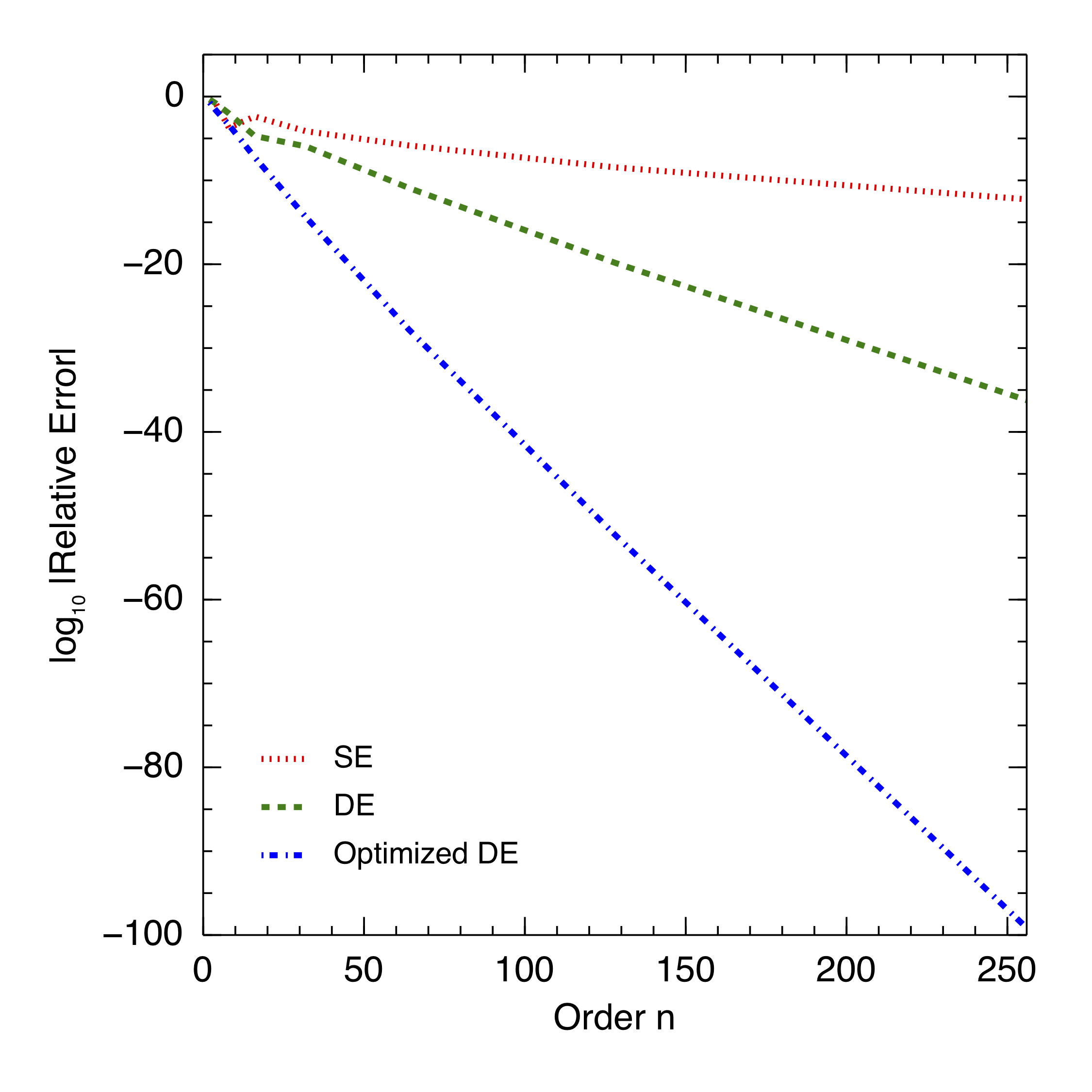
The simplest quadrature rule is the best: the trapezoidal rule. In the usual setting, we cannot expect a convergence rate better than \(\mathcal{O}(n^{-2})\), where \(n\) is the number of grid points. However, when the integrand decays double exponentially, that is, when \(f(x) = \mathcal{O}(e^{-\alpha e^{-\beta|x|}})\) for large \(x\) for some \(\alpha,\beta>0\), then the trusty trapezoidal rule has a provedly near-geometric convergence rate \(\mathcal{O}(e^{-Cn/\log n})\) for some \(C>0\)! If you are thinking that this is a special scenario, you will be comforted to know that most integrands \(f:[-1,1]\to\mathbb{R}\) can be transformed to other integrands with double exponential decay by a variable transformation such as \[x = \tanh\left(\frac{\pi}{2}\sinh(t)\right).\quad\hbox{Try it!}\] Why do we care? Other quadrature alternatives require expensive computations for the nodes and the weights; on the other hand, the trapezoidal rule's nodes are equispaced and the weights are equal. This makes high precision calculations a breeze! In my paper with Sheehan Olver, we consider further optimizing the geometric convergence rate when the integrand has singularities in the complex plane that are near the interval of integration. The problem is formulated as an infinite-dimensional constrained nonlinear program: we optimize the convergence rate over all eligible variable transformations. Singularities in the complex plane are the silent killers of an integral; tackling them head-on, we improve the reliability of the exponentially convergent trapezoidal rule.