Lecture 4, part 1 of 2
| PLNT4610/PLNT7690
Bioinformatics Lecture 4, part 1 of 2 |
Pearson WR (1998) Flexible sequence similarity searching with the FASTA3 program package. http://people.virginia.edu/~wrp/papers/mmol98f.pdf
1. Similarity between two sequences can be detected as a diagonal on an identitiy matrix.
2. Similarity comparisons can be speeded up using lookup tables containing positions of short words (oligomers) from one of the sequences.
3. Similarity searches can also be used to detect direct repeats and inverted repeats.
1. Global sequence alignment by dynamic programming
2. Scoring matrices
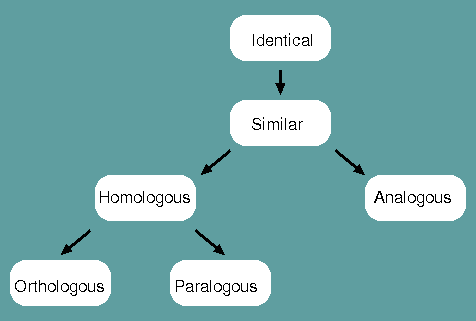
Identical - When a corresponding character is shared between two species or populations, that character is said to be identical.
Similar - The degree to which two species or populations share identities.
Homologous - When characters are similar due to common ancestry, they are homologous.
Analogous - When characters are similar due to convergent evolution, they are analogous.
Orthologous - When characters are homologous with conserverd function, they are orthologous.
Paralogous - When characters are homologous with divergent function, they are paralogous.
Homology is therefore NOT synonomous with similarity. Homology is a judgement, similarity is a measurement.
Graphic similarity
comparisons use the power of the computer to present
relationships between sequences in such a graphic form that
enables the human researcher to discern patterns in the data. If
we wish to determine whether two sequences are similar, we must
compare all parts of one sequence with all parts of the other.
This could be accomplished by sliding one sequence along
the other and noting the number of identities at each alignment.
The alignment with the greatest number of identities would be
the optimal alignment.
GGCTTGACCGG--> |
GGCTTGACCGG--> |
GGCTTGACCGG--> |
The same thing could be
accomplished by placing both sequences on the X and Y axes of a
matrix, and printing a character at each X,Y coordinate at which
both sequences have identical bases.
| G | G | C | T | T | G | A | C | C | G | G | |
| G | A | A | A | A | A | ||||||
| G | A | A | A | A | A | ||||||
| A | A | ||||||||||
| T | A | A | |||||||||
| T | A | A | |||||||||
| G | A | A | A | A | A | ||||||
| A | A | ||||||||||
| C | A | A | A | ||||||||
| C | A | A | A | ||||||||
| C | A | A | A | ||||||||
| G | A | A | A | A | A |
This is the simplest
form of a "dot-matrix" comparison. Where part of one sequence
shares a long stretch of similarity with the other sequence, a
diagonal of dots will be evident in the matrix. This approach is
exhaustive, because the matrix encompasses all possible
alignments. However, when single bases are compared at each
position, most of the dots in the matrix will be due to
background similarity. That is, for any two nucleotides compared
between the two sequences, there is a 1 in 4 chance of a match,
assuming equal frequencies of A,G,C and T.
| ALGORITHM Dot-matrix comparison, l=1 |
input: Sequences: s of length m, t of length n for i = 1..m // for each nucleotide in s if s[i] = t[j] then |
This background noise
can be filtered out by comparing groups of l nucleotides,
rather than single nucleotides, at each position. For example,
if we compare dinucleotides (l = 2), the probability of
two dinucleotides chosen at random from each sequence matching
is 1/16, rather than 1/4. Therefore, the number of background
matches will be lower:
| G | G | C | T | T | G | A | C | C | G | G | |
| G | A | A | |||||||||
| G | A | ||||||||||
| A | |||||||||||
| T | A | ||||||||||
| T | A | ||||||||||
| G | A | ||||||||||
| A | A | ||||||||||
| C | A | ||||||||||
| C | A | ||||||||||
| C | A | ||||||||||
| G |
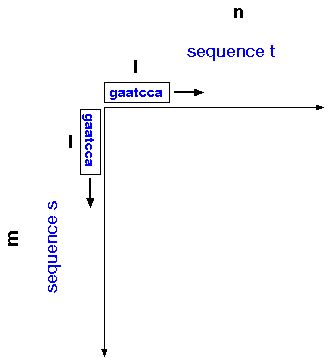
The dot-matrix algorithm
can be generalized for sequences s and t of
sizes m and n, respectively, and window size
l. For each position in sequence s, compare
a window of l nucleotides centered at that position
with each window of l nucleotides in sequence t.
Conceptually, you can think of windows of length l sliding along
each axis, so that all possible windows of l nucleotides are
compared between the two sequences.
For sequences of realistic length, it's not practical to write both sequences on the axes, so instead numbers are used to represent position in each sequence. Also for longer sequences, a window size of l=2 is too small, because as sequences increase in length, the frequencies of dinucleotide matches will increase.
Example: Comparison of two soybean chlorophyll a/b binding protein genes (X12980, X12981)
In the example, a
compression of 25 is used, meaning that each row and column in
the matrix represents 25 nucleotides, so that each cell
represents 252 = 625 comparisons of l =
20 nucleotides. The diagonal encompasses most of the matrix,
indicating that these two genes share strong similarity over
most of their length. In this example, the Minimum Percent
Similarity is set to 60, meaning that for a character to be
printed in the matrix, a given 20 nucleotide window must be at
least 60% identical between the two sequences (ie. 12 out of
20). To indicate the quality of each match, a character code is
used:
| Char. | % | Char. | % | Char. | % | Char. | % |
| A | 100 | N | 74-75 | a | 48-49 | n | 22-23 |
| B | 98-99 | O | 72-73 | b | 46-47 | o | 20-21 |
| C | 96-97 | P | 70-71 | c | 44-45 | p | 18-19 |
| D | 94-95 | Q | 68-69 | d | 42-43 | q | 16-17 |
| E | 92-93 | R | 66-67 | e | 40-41 | r | 14-15 |
| F | 90-91 | S | 64-65 | f | 38-39 | s | 12-13 |
| G | 88-89 | T | 62-63 | g | 36-37 | t | 10-11 |
| H | 86-87 | U | 60-61 | h | 34-35 | u | 9-8 |
| I | 84-85 | V | 58-59 | i | 32-33 | v | 6-7 |
| J | 82-83 | W | 56-57 | j | 30-31 | w | 5 |
| K | 80-81 | X | 54-55 | k | 28-29 | ||
| L | 78-79 | Y | 52-53 | l | 26-27 | ||
| M | 76-77 | Z | 50-51 | m | 24-25 | ||
| Pustell J and Kafatos F (1982) A high speed, high capacity similarity matrix: zooming through SV40 and polyoma Nucl. Acids Res. 10: 4765-4782. | |||||||
Because users already know the order of letters in the alphabet, the character codes provide an intuitive picture of the quality of the match in all parts of the sequences. In the example, the presence of A's in the diagonal from about 825 to 875 in both sequences shows that this region is highly conserved, whereas similarity drops off outside of this region. The first 250 bases of both sequences show little similarity. The GenBank entries indicate that the protein coding sequence begins at 251 in each sequences. Thus, the 5' non-coding regions of these genes must be poorly conserved.
A quick inspection of most matrix similarity outputs shows that the vast majority of the area of the matrix contains either blank space, which indicates that no local similarities were found, or very small similarities which have probably occurred at random. Thus, the majority of the search time is spent investigating regions of non-similarity.
Wilbur and Lipman
(1983) have recognized the fact that even
imperfect similarities are likely to
share small regions of perfect similarity (eg.
4 bases). Given the probability p of any two
characters matching, the probability that two k-mers
chosen at random is simply pk. The expected
distance between two occurrences of k matches is
therfore 1/pk. For example, if the
probability of a single nucleotide match is 1/4, then
trinucleotides should match on the average of once every
64 bases. These matches are due to background similarity.
Since regions which share significant similarity must by
definition have a frequency of matches which is higher than
background, similar regions will have more frequent k-mer
matches, and are consequently more likely to be found. If,
when searching the X-axis sequence, we knew in advance where
matches of k nucleotides occurred, we might only look at
those places to find out if the match extended to a length of l
nucleotides. It can be shown that a lookup table of k-mers
in
any
sequence can be can be constructed in O(n) steps. An
example of a lookup table for trinucleotides is shown below:
| Table 1.
Example of a Lookup Table
Locations of the 64 possible trinucleotides in sequence X. The numbers shown indicate the position of the central nucleotide in a triplet, as they might occur in some hypothetical DNA sequence. |
|
| Trinucleotide | Location(s) in seq.X |
| AAA | 13, 71, 179, 204, ... |
| AAC | 35, 72, 123, 199, ... |
| AAG | 7, 50, 87, 104, 249, ... |
| ... | ....... |
| ... | ....... |
| TTG | 2, 40, 95, 172, ... |
| TTT | 77, 94, 169, 195, ... |
Using the table as a guide, each occurrence of that trinucleotide in sequence X is located, and the region centered on that position, w nucleotides to the left and the right, is compared with the corresponding region in sequence Y. If the match is good enough, a symbol is printed at the point in the matrix which corresponds to the centers of the two regions. The process is repeated for each trinucleotide in sequence Y. Since each trinucleotide occurs on the average only once every 64 bases, the algorithm only makes N/64 searches for each triplet in Y, rather than N. Generally, the efficiency of this algorighm is O(lmn/Sk), where S is the alphabet size. For nucleic acids, S=4 (A,G,C,T), so a trinucleotide search would provide a 64-fold increase in speed, while a tetranucleotide search provides a 256-fold speedup. For amino acid sequences, S=20, so a a search set to k=1 provides a 20-fold increase in speed, while k=2 provides a 400-fold increase.
In essence, the lookup
table speeds up the search by sampling the X-axis sequence where
perfect oligomer matches occur, rather than exhaustively
comparing every possible window of l nucleotides between two
sequences. The algorithm can be summarized thus:
| ALGORITHM Dot-matrix comparison, k=3 |
input: Sequences: s of length m, t of length n |
To ensure a thorough
search, we must choose a combination of k value
and window size such that the window l bases wide
which is searched at one k-mer match
will overlap the adjacent
window. The average distances between k-matches
for different values of p and k are
given in Table 2.
| Table 2. | Avg. dist. between
k-matches
1 |
|||
| Prob. of a match (p) | k= 2 | 3 | 4 | 5 |
| 0.050 | 400 | 8000 | ||
| 0.075 | 178 | 2370 | ||
| 0.100 | 100 | 1000 | ||
| 0.150 | 44 | 296 | ||
| 0.200 | 25 | 125 | ||
| 0.250 | 16 | 64 | 256 | 1024 |
| 0.300 | 11 | 37 | 123 | 412 |
| 0.350 | 8 | 23 | 67 | 190 |
| 0.450 | 5 | 11 | 24 | 54 |
| 0.600 | 3 | 5 | 8 | 13 |
| 0.700 | 2 | 3 | 4 | 6 |
| 0.900 | 1 | 1 | 1 | 2 |
For example, if the probability of a match between two DNA sequences is 0.25, we expect to see a dinucleotide match once every 16 bases in a comparison. Trinucleotides will match on the average of once every 64 bases, and so on. These matches are due to background similarity. Since regions which share significant similarity must by definition have a frequency of matches which is higher than background, similar regions will have more frequent k-mer matches, and consequently are more likely to be found.
Table 2 illustrates how the overall level of similarity between two sequences affects the expected distance between k-mer matches. The knowledge of the expected frequency of k-mer matches allows us to predict the level of similarity likely to be missed. If we wish to find nucleotide similarities with 30% match or better, a triplet search (k=3) will necessitate the use of a window size l >= 19, since the average distance between triplet matches is 37. The actual choice of k and l values will depend on the purpose of the search.
D3HOM Version 5/13/91 |
A more interesting example is seen in human sequence p16, which contains both an AluI family sequence, as well as eight tandem repeats, which themselves are made up of two imperfect repeats:
Human clone p16 (GenBank K01154)
Self comparison of p16 (low resolution)
Self comparison of p16 (high
resolution, 66nt repeats only)
 Unless otherwise cited or
referenced, all content on this page is licensed under
the Creative Commons License Attribution
Share-Alike 2.5 Canada Unless otherwise cited or
referenced, all content on this page is licensed under
the Creative Commons License Attribution
Share-Alike 2.5 Canada |
| PLNT4610/PLNT7690
Bioinformatics Lecture 4, part 1 of 2 |