Platonic solids

Back to top

Cube

Six square faces: two each of ebony, cocobolo, and bubinga.

Dodecahedron

Twelve pentagonal faces made of oak, black walnut, chokte kok, narra, mahogany, ebony, zircote, osage orange, birdseye maple, bubinga, purple heart, and cherry.

Icosahedron

Four faces each of kingwood, birdseye maple, bocote, cocobolo, and santos rosewood. All five woods meet at each vertex.

Octahedron

Four faces each of chestnut and bocote.

Tetrahedron

Four faces: one each of tulipwood, purple heart, padauk, and ebony.

Hollow with 5 inch edge lengths. Made from maple.

Archimedean Solids

Back to top

Cuboctahedron

Fourteen faces: eight triangles made from chestnut and 6 squares made from ebony.

Great rhombicosadodecahedron

Sixty-two faces: 12 decagons made from maple veneer on plywood, 30 squares made from walnut, and 20 hexagons made from cherry.

Great rhombicuboctahedron

Twenty-six faces: 12 squares made from zircote, 8 hexagons from osage orange (bowwood), and 6 octagons from bubinga.

Icosidodecahedron

Thirty-two faces: 20 triangles made from mahogany and 12 pentagons made from maple.

Lesser rhombicosadodecahedron

Sixty-two faces: 12 pentagons made from chokte kok, 20 triangles from kingwood, and 30 squares from cherry.

Lesser rhombicuboctahedron

Twenty-six faces: 18 squares made from teak and 8 triangles from tulipwood.

Snub cube

Thirty-eight faces: 32 triangles made from purple heart and maple and 6 squares from hickory.

Snub dodecahedron

Ninety-two faces: 80 triangles and 12 pentagons made from walnut.

Truncated cube

Fourteen faces: 6 octagons made from bubinga and 8 triangles from maples.

Truncated dodecahedron

Thirty-two faces: 20 triangles made from walnut and 12 decagons from mahogany. Made entirely from recovered wood: the mahogany planks were once bookshelves.

Truncated icosahedron

Thirty-two faces: 12 pentagons made from walnut and 20 hexagons from maples.

Truncated octahedron

Fourteen faces: 6 squares and 8 hexagons, all made from bloodwood.

Truncated tetrahedron

Eight faces: 4 hexagons made from purple heart and 4 triangles from lemon heart (pau amarello).

Open-faced da Vinci models

Back to top

Set of 5 open-faced Platonic solids

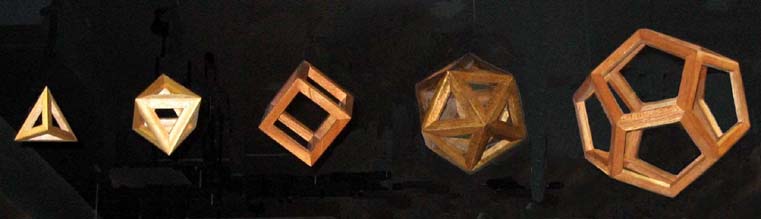
Each of these models is made with 5-inch edge lengths and all models are made from mahongany with 12, 12, 24, 60, and 60 pieces respectively.

Open-faced rhombicuboctahedron

Made from 96 pieces of pine, entirely recovered wood.

Open-faced Campanus sphere

Made from 264 pieces of obeche (also known as wawa).

Open-faced truncated icosahedron

Made from 180 pieces of wenge. Each face has the pieces of the polygon dowelled together at the joints and all face-face joints (except two) are biscuit-joined. To test the strength of this model, I once did a handstand on it.

The construction of this model is documented here.

Open-faced icosidodecahedron

Made from 120 pieces of Goncalo Alves (also known as tigerwood). This model is on display in the Department of Mathematics office.

My first open-faced icosidodecahedron, also made from tigerwood. This model was presented to Godfried Toussaint as a 60th birthday gift.

Open-faced stellated octahedron

Made of cherry, 5 inch edge lengths. Based on the following drawing by Da Vinci.

Truncation

Back to top

Truncating the cube

Five pieces: all solid and cut from one piece of cherry.

Truncating the cuboctahedron

A cuboctahedron truncated to give a great rhombicuboctahedron. Both pieces are made from solid mahogany and are roughly 2 inches in diameter.

Truncating the tetrahedron

Two pieces made from solid cherry.

Truncated dodecahedron

Approximately 2 inches in diameter, wood from a crabapple tree.

Other polyhedra

Back to top

Rhombic Triacontahedron

Thirty faces made from tigerwood, approximately 3/4 inches thick.

Icosahedron and dodecahedron

The icosahedron is made of solid maple and the dodecahedron from solid mahogany. Both are approximately 2.5 inches high.

Truncated cube, cuboctahedron, rhombicuboctahedron, and octahedron

Dissected cube

Two identical pieces made from oak.

Tetrahedron inscribed in a cube

Made from coffee sticks.

Icosahedron

Vertices are corners of three golden rectangles that appear to go through each other (an impossible structure).

Pentagonal antiprism

Solid, possibly made from silky oak.

Golden crystal

My own invention: each face is either a golden rectangle or a golden triangle, of which there are two types. Made from solid MDF, painted gold and varathaned.

Pentagonal trapezohedron

Made from 10 pieces of one inch thick obeche. Face angles are 108° and 36° and all dihedral angles are the same. This is sometimes mistakenly called a pentagonal deltohedron. This is the dual polyhedron for the pentagonal antiprism.

Space-filling solids

Back to top

Rhombhex dodecahedra

Seventeen pieces made from cherry and walnut in a plexiglass case.

Made from solid oak.

Cuboctahedra

Seventeen pieces: made from an unknown rare wood.

Rhombic dodecahedron

Made from walnut.

Rhombic dodecahedron constructed from an inner cube, perhaps made from aspen, and six cherry pyramids attached with dowels.

Hexagonal prisms

Around twenty pieces made from solid oak. All edge lengths are 1 inch.

Parallelepipeds

Six or more pieces: Rhombic parallelepipeds made from spruce with all edge lengths the same. Approximately 2 inches high.

K-dron

Ten pieces made from solid cherry, approximately 2 inches high.

Penrose tiles

Approximately 300 pieces, each made form two golden triangles. This set was donated to the Math Club.

Puzzles

Back to top

Dovetail

Made from walnut and beech.

Drive ya crazy

Made from purpleheart and tulipwood. Awarded as first prize for the High School Math Workshop in January 2004.

Case is made from ebony and bloodwood. Hidden door, attached with magnets, and hidden compartment for solutions. Inside are six cubes each with six colours.

Hole in a triangle

Four movable pieces of maple in a mahogany case.

Frame made from maple, base from purpleheart, two pieces from cherry, and two mahogany.

O'Beirne's melting box

Four teak and five mahogany blocks. The case is made from maple and walnut.

Pentominoes

Twelve mahogany pieces in a mahogany case.

Sliding box puzzle

Made from zircote and bloodwood.

World's hardest two-piece puzzle

Three pieces of rosewood and the case is made of walnut. My own design: an extension of the standard two piece dissection of the tetrahedron.

Towers of Hanoi

Disks made from gaboon ebony and the base is made from vera wood.

Dissections

Back to top

Square-triangle hinged dissection

Mahogany and brass hinges.

Pentagon-triangle hinged dissection

Mahoany with brass hinges. Approximately 6 inches across.

Hexagon-triangle hinged dissection

Made from mahogany, probably African mahogany. Tape hinges.

Copies of the pentagon-triangle and hexagon-triangle dissection were made for Greg Frederickson. They can be seen at his website.

Paper models

Back to top

Kepler-Poinsot solids

Small stellated dodecahedron, great icosahedron, great stellated dodecahedron, and the great dodecahedron

Csaszar polyhedron

Seven vertices, each pair joined by an edge.

Szilassi polyhedron

Seven faces, each pair share an edge.

Rhombic tricontahedron

Pentagonal deltohedron

14th stellation of the icosahedron

Others

Four folded polyhedra. The orange figure is a compound of two cubes.

Miscellaneous pieces

Back to top

Hexaflexahedron

Six tetrahedra made from solid cherry, connected with brass hinges.

Four triangles interlocking

Made from santos rosewood, chakte kok, kingwood, and birdseye maple. Modelled after a carboard version that appeared on the cover of The Mathematical Intelligencer.

Trefoil knot

Hand carved from bloodwood.

Enantiomorphic pair of `cubic' trefoil knots, each made from 1 × 1 × 2 blocks.

Möbius band

Five layers of laminated maples veneer, invisible seams.

Hyperboloid of one sheet

Made from oak dowels with top and bottom made from MDF.

Plug filling three holes

Template made from bloodwood and the plug is made from oak.

Trammel

Cherry base, rosewood arm, mahogany slide and solid brass handle (which moves in an ellipse).

Initial blocks

Approximately 2 inches high; perhaps maple.

Made from solid mahogany.

Mutually orthogonal latin squares

Twenty triangles each of bubinga, zebrawood, lemonwood (pau feraro), padauk, and grey elm. Frame and inserts made from walnut.

Nailless Nailbanger's Nightmare

Spruce pieces fitted together without nails or glue. It is a partially finished 'nailless' version of George Hart's Nailbanger's Nightmare. This model was featured in an article by George Hart for his Math Monday column.