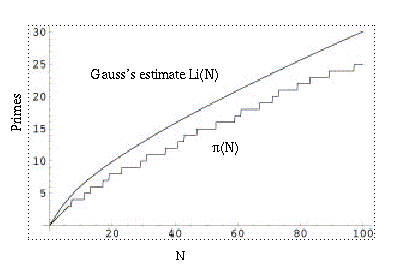
Prime Counting:
What have we got:
- Riemann Zeta Function, the analytical extension of the generalized harmonic series.
- Fourier series.
Riemann noticed that he could
approximate the
prime counting function by a term by term accumulation of basis
functions. The
prime counting function will be the sum of tones of slightly more
complicated waves than sinusoids.
Ultimately at some infinitely distant point the simultaneous
construction gives
a perfect replication of the prime distribution function, and hence the
prime
counting function.
|
|
|


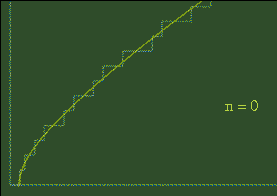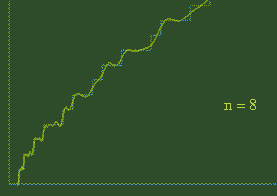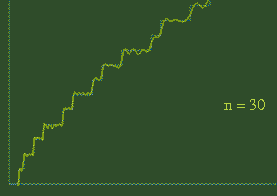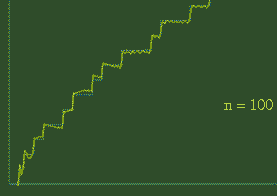
Obviously these figures were bootlegged from various sources.
Here is something interesting about zeros of complex functions. If you
find web
sites showing the calculation of zeros of the Zeta function they tend
to look
like this. Z(t) is a cousin of Zeta(s) with zeros along the critical
line
This is a bit
confusing
because it is not clear that there would not be zeros just off the
critial
line.
Aside: The formula to calculate
Z(t) was
discovered by Riemann and rediscovered by Siegel and published in the
1930s O(t1/2).
Prior Z(t) utilized a method denoted Euler-Maclaurin which is similar
to that
used by Ramanujan O(t).
When looking at zeros of a complex function of a complex of a complex
variable,
both real and imaginary parts simultaneously are required to be zero.
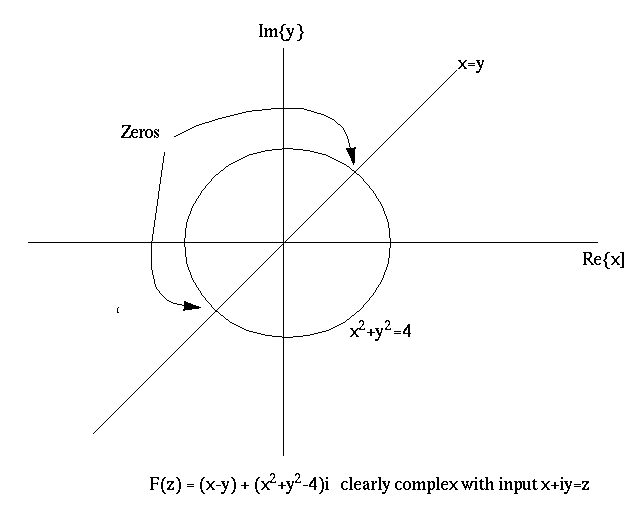
Density of the Zeros
Riemann conjectured that the density of Zeta zeros was approximately
log(T/2p)
Reciprocal to the density of Primes!
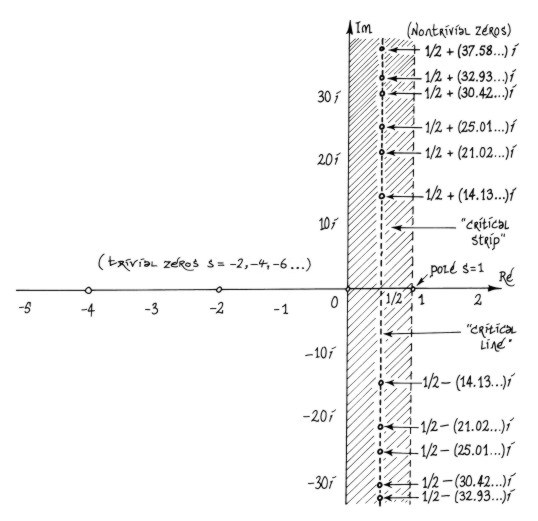
The zeros are getting closer togther as one one heads up the critical line, real part =1/2. Reimann had already proved the non trivial zeros were confined to the critical strip.