1850 Riemann
The Schubert of Mathematics.


Looked a bit like
Maxwell.
1851: Riemann's thesis
studied the theory of complex variables. The work builds
on
Cauchy's foundations of the theory of complex variables built up over
many
years and also on Puiseux's ideas of branch points. However, Riemann's
thesis
is a strikingly original piece of work which examined geometric
properties of
analytic functions, conformal mapping and the connectivity of surfaces.
1854: Gave a
lecture to begin lecturing, it
became a classic of mathematics.
There were two parts to Riemann's lecture. In the first part he posed the problem what today is called a Riemannian space.
It possesses shortest lines, now called geodesics, which resemble ordinary straight lines. Beings living in a space may discover the curvature of their world and compute it at any point as a consequence of observed deviations from Pythagoras' theorem.
The second part of Riemann's lecture posed deep questions about the relationship of geometry to the world we live in. He asked what the dimension of real space was and what geometry described real space. The lecture was too far ahead of its time to be appreciated by most scientists of that time.
1859: Newly elected to the Berlin
Academy
of Sciences Riemann sent a report on
On the number of primes less than a given magnitude
that changed the direction of mathematical research in a most significant way.
(s) =
(1/ns) =
(1 - p-s)-1
Riemann looked at the zeta function
as a
complex function rather than a real one.
Except for a few trivial (no complex part) exceptions, the roots of ![]() (s) all lie
between 0 and 1. The critical strip.
(s) all lie
between 0 and 1. The critical strip.
- In the paper, he stated that the zeta function had infinitely many nontrivial roots and that it seemed probable that they all have real part 1/2.
- This is the famous Riemann hypothesis, one of the most important of the unsolved problems of mathematics.
Apparently Riemann did not present any zeros in the paper leading others to speculate that he didn't calculate any.
- It appears that he did, as a method of their calculation was determined by Siegel (1932) from a through review of Riemann's unpublished diary, the Nachlass. It is believed Riemann calculated 3 roots.
1866: Riemann died at age 39, hence the Schubert analog.
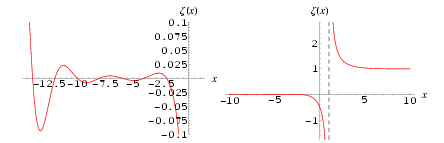
Note: The above shows some trivial zero's for the analytical extension
of the
zeta function.
Note: Another incarnation of the Zeta function
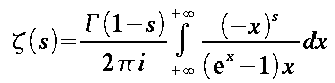
The integration looks a little funny.
The value at -1 will come back later, as it was this calculation that brought Ramanujan to Hardy . At x = -1, Zeta(-1) has some value (-1/12).
Aside: Fourier