Gauss (1810) Quentin Tarantino Style

Also liked hats.
One of the first to conjecture the distribution of primes, i.e. the
Prime
Number Theorem when he was 15. After being given a book
on
logarithms (Scottish invention Napier 1614), that included an unrelated
table of primes.
Legendre actually first published an
estimate for
the rate of growth of the primes.
Gauss noted that the density of primes near any given number was
approximately
the reciprocal of its logarithm.
As such, Gauss was able to estimate the number of primes by integrating
over
the density.
Prime counting function is given by the logarithmic integral. Li(x)


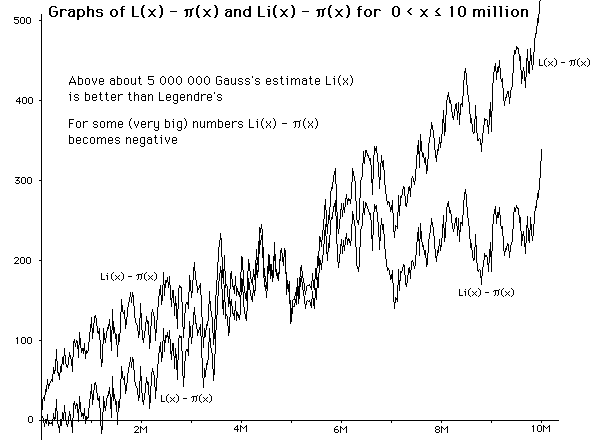
Legendre's estimate was a dead end, Guass's was in the right direction.
The (very big) number mentioned
above
will return to the story.
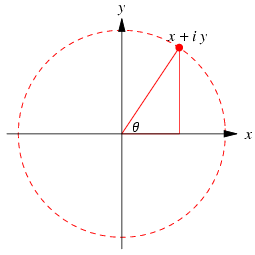
Another unpublished discovery made by Gauss, was the representation of
complex
numbers in the complex plane. Discovered by Wessel (Surveyor) and
Argand (Bookkeeper).
Gauss Proved: The Fundamental Theorem of Arithmetic or the Fundamental principle of number theory which states
Any integer greater than 1 can be expressed as the product of prime numbers in only one way.
A corollary of the first of Euclid's theorems
Gauss had a quote for NSERC: The total number of Dirichlet's
publications is
not large: jewels are not weighed on a grocery scale.
Pauca sed matura [His motto:]
Few, but ripe.
Prodigy: At 7 summed the numbers 1 to 100 in his head = 5050.
Aside 1: Erdos was the oldest child prodigy, source of the Erdos
number which is the analog of the Kevin Bacon number.