Wikipedia Near Sets

http://en.wikipedia.org/wiki/Near_sets

Near sets are either spatially close or descriptively close. Spatially close sets have nonempty intersection. In other words, spatially close sets are not disjoint sets, since they always have at least one element in common. Descriptively close sets contain elements that have matching descriptions. Such sets can be either disjoint or non-disjoint sets. Spatially near sets are also descriptively near sets.

The underlying assumption with descriptively close sets is that such sets contain elements that have location and measurable features such as colour and frequency of occurrence. The description of the element of a set is defined by a feature vector. Comparison of feature vectors provides a basis for measuring the closeness of descriptively near sets. Near set theory provides a formal basis for the observation, comparison, and classification of elements in sets based on their closeness, either spatially or descriptively. Near sets offer a framework for solving problems based on human perception that arise in areas such as image processing, computer vision as well as engineering and science problems.

Near sets have a variety of applications in areas such as topology, pattern detection and classification, abstract algebra, mathematics in computer science, and solving a variety of problems based on human perception that arise in areas such as image analysis, image processing, face recognition, ethology, as well as engineering and science problems. From the beginning, descriptively near sets have proved to be useful in applications of topology, and visual pattern recognition, spanning a broad spectrum of applications that include camouflage detection, micropaleontology, handwriting forgery detection, biomedical image analysis, content-based image retrieval, population dynamics, quotient topology, textile design, visual merchandising, and topological psychology.

As an illustration of the degree of descriptive nearness between two sets, consider an example of the Henry colour model for varying degrees of nearness between sets of picture elements in pictures (see, e.g., Henry, C.: Near Sets: Theory and Applications, Supervisor: J.F. Peters, Department of Electrical & Computer Engineering, University of Manitoba (2010), §4.3). The two pairs of ovals in Fig. 1 and Fig. 2 below contain coloured segments. Each segment in the figures corresponds to an equivalence class where all pixels in the class have similar descriptions, i.e., picture elements with similar colours. The ovals in Fig.1 are closer to each other descriptively than the ovals in Fig. 2.

Contents

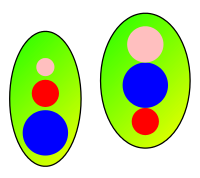Figure 1. Descriptively, very near sets

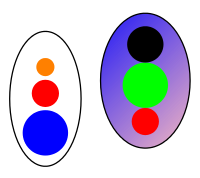Figure 2. Descriptively, minimally near sets